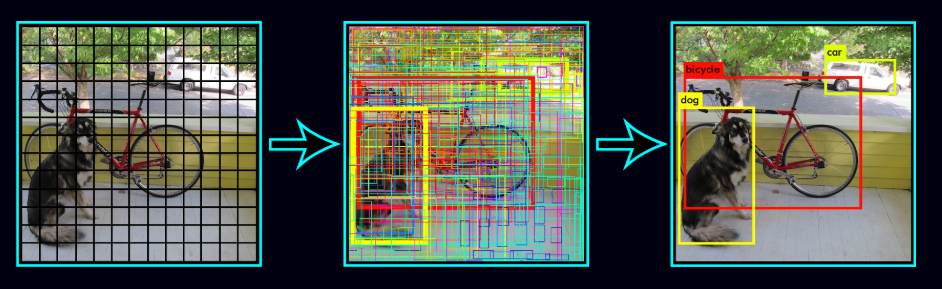
Object detection for self-driving cars

In the previous blog, Introduction to Object detection, we learned the basics of object detection. We also got an overview of the YOLO (You Look Only Once algorithm). In this blog, we will extend our learning and will dive deeper into the YOLO algorithm. We will learn topics such as intersection over area metrics, non maximal suppression, multiple object detection, anchor boxes, etc. Finally, we will build an object detection detection system for a self-driving car using the YOLO algorithm. We will be using the Berkeley driving dataset to train our model.

Data Preprocessing

Before, we get into building the various components of the object detection model, we will perform some preprocessing steps. The preprocessing steps involve resizing the images (according to the input shape accepted by the model) and converting the box coordinates into the appropriate form. Since we will be building a object detection for a self-driving car, we will be detecting and localizing eight different classes. These classes are ‘bike’, ‘bus’, ‘car’, ‘motor’, ‘person’, ‘rider’, ‘train’, and ‘truck’. Therefore, our target variable will be defined as:

where,

\begin{equation}
\hat{y} ={
\begin{bmatrix}
{p_c}& {b_x} & {b_y} & {b_h} & {b_w} & {c_1} & {c_2} & … & {c_8}
\end{bmatrix}}^T
\end{equation}

p_c : Probability/confidence of an object being present in the bounding box

b_x, b_y : coordinates of the center of the bounding box

b_w : width of the bounding box w.r.t the image width

b_h : height of the bounding box w.r.t the image height

c_i = Probability of the i_th class

But since the box coordinates provided in the dataset are in the following format: x_min, y_min, x_max, y_max (see Fig 1.), we need to convert them according to the target variable defined above. This can be implemented as follows:

W : width of the original image
H : height of the original image

\begin{equation}
b_x = \frac{(x_{min} + x_{max})}{2 * W}\ , \ b_y = \frac{(y_{min} + y_{max})}{2 * H} \\
b_w = \frac{(x_{max} – x_{min})}{2 * W}\ , \ b_y = \frac{(y_{max} + y_{min})}{2 * W}
\end{equation}

def process_data(images, boxes=None):
    """
    Process the data
    """
    images = [PIL.Image.fromarray(i) for i in images]
    orig_size = np.array([images[0].width, images[0].height])
    orig_size = np.expand_dims(orig_size, axis=0)
    
    #Image preprocessing 
    processed_images = [i.resize((416, 416), PIL.Image.BICUBIC) for i in images]
    processed_images = [np.array(image, dtype=np.float) for image in processed_images]
    processed_images = [image/255. for image in processed_images]
    
    if boxes is not None:
        # Box preprocessing
        # Original boxes stored as as 1D list of class, x_min, y_min, x_max, y_max
        boxes = [box.reshape((-1, 5)) for box in boxes]
        # Get extents as y_min, x_min, y_max, x_max, class for comparison with 
        # model output
        box_extents = [box[:, [2,1,4,3,0]] for box in boxes]
        
        # Get box parameters as x_center, y_center, box_width, box_height, class.
        boxes_xy = [0.5* (box[:, 3:5] + box[:, 1:3]) for box in boxes]
        boxes_wh = [box[:, 3:5] - box[:, 1:3] for box in boxes]
        boxes_xy = [box_xy / orig_size for box_xy in boxes_xy]
        boxes_wh = [box_wh / orig_size for box_wh in boxes_wh]
        boxes = [np.concatenate((boxes_xy[i], boxes_wh[i], box[:, 0:1]), axis=-1) for i, box in enumerate(boxes)]
        
        # find the max number of boxes 
        max_boxes = 0
        for boxz in boxes:
            if boxz.shape[0] > max_boxes:
                max_boxes = boxz.shape[0]
        # add zero pad for training 
        for i, boxz in enumerate(boxes):
            if boxz.shape[0] <  max_boxes:
                zero_padding = np.zeros((max_boxes - boxz.shape[0], 5), dtype=np.float32)
                boxes[i] = np.vstack((boxz, zero_padding))
        
        return np.array(processed_images), np.array(boxes)
    else:
        return np.array(processed_images)

Intersection Over Union

Intersection over Union (IoU) is an evaluation metric that is used to measure the accuracy of an object detection algorithm. Generally, IoU is a measure of the overlap between two bounding boxes. To calculate this metric, we need:

• The ground truth bounding boxes (i.e. the hand labeled bounding boxes)
• The predicted bounding boxes from the model

Intersection over Union is the ratio of the area of intersection over the union area occupied by the ground truth bounding box and the predicted bounding box. Fig. 9 shows the IoU calculation for different bounding box scenarios.

Intersection over Union is the ratio of the area of intersection over the union area occupied by the ground truth bounding box and the predicted bounding box. Fig. 2 shows the IoU calculation for different bounding box scenarios.

Now, that we have a better understanding of the metric, let’s code it.

 
def IoU(box1, box2):
    """
    Returns the Intersection over Union (IoU) between box1 and box2
    
    Arguments: 
    box1: coordinates: (x1, y1, x2, y2)
    box2: coordinates: (x1, y1, x2, y2)
    """
    # Calculate the intersection area of the two boxes. 
    xi1 = max(box1[0], box2[0])
    yi1 = max(box1[1], box2[1])
    xi2 = min(box1[2], box2[2])
    yi2 = min(box1[3], box2[3])
    
    area_of_intersection = (xi2 - xi1) * (yi2 - yi1)
    
    # Calculate the union area of the two boxes
    # A U B = A + B - A ∩ B
    A = (box1[2] - box1[0]) * (box1[3] - box1[1])
    B = (box2[2] - box2[0]) * (box2[3] - box2[1])
    
    union_area = A + B - area_of_intersection
    
    intersection_over_union = area_of_intersection/ union_area
    
    return intersection_over_union

Defining the Model

Instead of building the model from scratch, we will be using a pre-trained network and applying transfer learning to create our final model. You only look once (YOLO) is a state-of-the-art, real-time object detection system, which has a mAP on VOC 2007 of 78.6% and a mAP of 48.1% on the COCO test-dev. YOLO applies a single neural network to the full image. This network divides the image into regions and predicts the bounding boxes and probabilities for each region. These bounding boxes are weighted by the predicted probabilities.

One of the advantages of YOLO is that it looks at the whole image during the test time, so its predictions are informed by global context in the image. Unlike R-CNN, which requires thousands of networks for a single image, YOLO makes predictions with a single network. This makes this algorithm extremely fast, over 1000x faster than R-CNN and 100x faster than Fast R-CNN.

Loss Function

If the target variable $# y $#  is defined as

\begin{equation}
y ={
\begin{bmatrix}
{p_c}& {b_x} & {b_y} & {b_h} & {b_w} & {c_1} & {c_2} & {…} & {c_8}
\end{bmatrix}}^T \\
\begin{matrix}
& {y_1}& {y_2} & {y_3} & {y_4} & {y_5} & {y_6} & {y_7} & {…} & {y_{13}}
\end{matrix}
\end{equation}

the loss function for object localization is defined as

\begin{equation}
\mathcal{L(\hat{y}, y)} =
\begin{cases}
(\hat{y_1} – y_1)^2 + (\hat{y_2} – y_2)^2 + … + (\hat{y_{13}} – y_{13})^2 &&, y_1=1 \\
(\hat{y_1} – y_1)^2 &&, y_1=0
\end{cases}
\end{equation}

The loss function in case of the YOLO algorithm is calculated using the following steps:

• Find the bounding boxes with the highest IoU with the true bounding boxes
• Calculate the confidence loss (the probability of object being present inside the bounding box)
• Calculate the classification loss (the probability of class present inside the bounding box)
• Calculate the coordinate loss for the matching detected boxes.
• Total loss is the sum of the confidence loss, classification loss, and coordinate loss.

Using the steps defined above, let’s calculate the loss function for the YOLO algorithm.

In general, the target variable is defined as

\begin{equation}
y ={
\begin{bmatrix}
{p_i(c)}& {x_i} & {y_i} & {h_i} & {w_i} & {C_i}
\end{bmatrix}}^T
\end{equation}

where, 

p_i(c) : Probability/confidence of an object being present in the bounding box.
x_i, y_i : coordinates of the center of the bounding box.
w_i : width of the bounding box w.r.t the image width.
h_i : height of the bounding box w.r.t the image height.
C_i = Probability of the i_th class.

then the corresponding loss function is calculated as

where,

The above equation represents the yolo loss function. The equation may seem daunting at first, but on having a closer look we can see it is the sum of the coordinate loss, the classification loss, and the confidence loss in that order. We use sum of squared errors because it is easy to optimize. However, it weights the localization error equally with classification error which may not be ideal. To remedy this, we increase the loss from bounding box coordinate predictions and decrease the loss from confidence predictions for boxes that don’t contain objects. We use two parameters, λ_coord and λ_noobj to accomplish this.

Note that the loss function only penalizes classification error if an object is present in that grid cell. It also penalizes the bounding box coordinate error if that predictor is responsible for the ground truth box (i.e which has the highest IOU of any predictor in that grid cell).

Model Architecture

The YOLO model has the following architecture (see Fig 3). The network has 24 convolutional layers followed by two fully connected layers. Alternating 1 × 1 convolutional layers reduce the features space from preceding layers. The convolutional layers are pretrained on the ImageNet classification task at half the resolution (224 × 224 input image) and then double the resolution for detection.

We will be using pre trained YOLOv2 model, which has been trained on the COCO image dataset with classes similar to the Berkeley Driving Dataset. So, we will use the YOLOv2 pretrained network as a feature extractor. We will load the pretrained weights of the YOLOv2 model and will freeze all the weights except for the last layer during training of the model. We will remove the last convolutional layer of the YOLOv2 model and replace it with a new convolutional layer indicating the number of classes (8 classes as defined earlier) to be predicted. This is implemented in the following code.

 
def create_model(anchors, class_names, load_pretrained=True, freeze_body = True):
    """
    
    load_pretrained: whether or not to load the pretrained model or initialize all weights

    freeze_body: whether or not to freeze all weights except for the last layer
    
    Returns:
    model_body : YOLOv2 with new output layer
    model : YOLOv2 with custom loss Lambda layer  
    
    """
    detector_mask_shape = (13, 13, 5, 1)
    matching_boxes_shape = (13, 13, 5, 5)
    
    # Create model input layers 
    image_input = Input(shape=(416,416,3))
    boxes_input = Input(shape=(None, 5))
    detector_mask_input = Input(shape=detector_mask_shape)
    matching_boxes_input = Input(shape=matching_boxes_shape)
    
    # Create model body
    yolo_model = yolo_body(image_input, len(anchors), len(class_names))
    topless_yolo = Model(yolo_model.input, yolo_model.layers[-2].output)
    
    if load_pretrained == True:
        # Save topless yolo
        topless_yolo_path = os.path.join('model_data', 'yolo_topless.h5')
        if not os.path.exists(topless_yolo_path):
            print('Creating Topless weights file')
            yolo_path = os.path.join('model_data', 'yolo.h5')
            model_body = load_model(yolo_path)
            model_body = Model(model_body.inputs, model_body.layers[-2].output)
            model_body.save_weights(topless_yolo_path)
        topless_yolo.load_weights(topless_yolo_path)
        
    if freeze_body:
        for layer in topless_yolo.layers:
            layer.trainable = False
    
    final_layer = Conv2D(len(anchors)*(5 + len(class_names)), (1, 1), activation='linear')(topless_yolo.output)
    model_body = Model(image_input, final_layer)
    
    # Place model loss on CPU to reduce GPU memory usage.    
    with tf.device('/cpu:0'):
        model_loss = Lambda(yolo_loss, output_shape=(1,), name='yolo_loss', arguments={
            'anchors': anchors, 
            'num_classes': len(class_names)})([model_body.output, boxes_input, detector_mask_input, matching_boxes_input])
    
    model = Model([model_body.input, boxes_input, detector_mask_input, matching_boxes_input], model_loss)
    return model_body, model

Due to limited computational power, we used only the first 1000 images present in the training dataset to train the model. Finally, we trained the model for 20 epochs and saved the model weights with the lowest loss.

Tackling Multiple Detection

Threshold Filtering

The YOLO object detection algorithm will predict multiple overlapping bounding boxes for a given image. As not all bounding boxes contain the object to be classified (e.g. pedestrian, bike, car or truck) or detected, we need to filter out those bounding boxes that don’t contain the target object. To implement this, we monitor the value of p_c, i.e., the probability or confidence of an object (i.e. the four classes) being present in the bounding box. If the value of p_c is less than the threshold value, then we filter out that bounding box from the predicted bounding boxes. This threshold may vary from model to model and serve as a hyper-parameter for the model.

If predicted target variable is defined as:

\begin{equation}
\hat{y} ={
\begin{bmatrix}
{p_c}& {b_x} & {b_y} & {b_h} & {b_w} & {c_1} & {c_2} & … & {c_8}
\end{bmatrix}}^T
\end{equation}

then discard all bounding boxes where the value of p_c < threshold value. The following code implements this approach.

 
def yolo_filter_boxes(box_confidence, boxes, box_class_probs, threshold=0.6):
    """
    Filters YOLO boxes by thresholding on object and class confidence
    Arguments: 
    box_confidence: Probability of the box containing the object
    boxes: The box parameters : (x, y, h, w) 
           x, y -> Center of the box 
           h, w -> Height and width of the box w.r.t the image size
    box_class_probs: Probability of all the classes for each box
    threshold: Threshold value for box confidence
    
    Returns: 
    scores: containing the class probability score for the selected boxes
    boxes: contains box coordinates for the selected boxes
    classes: contains the index of the class detected by the selected boxes
    """
    
    # Compute the box scores: 
    box_scores = box_confidence * box_class_probs
    
    # Find the box classes index with the maximum box score
    box_classes = K.argmax(box_scores)
    # Find the box classes with maximum box score
    box_class_scores = K.max(box_scores, axis=-1)
    
    # Creating a mask for selecting the boxes that have box score greater than threshold
    thresh_mask = box_class_scores >= threshold
    # Selecting the scores, boxes and classes with box score greater than 
    # threshold by filtering the box score with the help of thresh_mask.
    scores = tf.boolean_mask(tensor=box_class_scores, mask=thresh_mask)
    classes = tf.boolean_mask(tensor=box_classes, mask=thresh_mask)
    boxes = tf.boolean_mask(tensor=boxes, mask=thresh_mask)
    
    return scores, classes, boxes

Non-max Suppression

Even after filtering by thresholding over the classes score, we may still end up with a lot of overlapping bounding boxes. This is because the YOLO algorithm may detect an object multiple times, which is one of its drawbacks. A second filter called non-maximal suppression (NMS) is used to remove duplicate detections of an object. Non-max suppression uses ‘Intersection over Union’ (IoU) to fix multiple detections.

Non-maximal suppression is implemented as follows:

• Find the box confidence (p_c) (Probability of the box containing the object) for each detection.
• Pick the bounding box with the maximum box confidence. Output this box as prediction.
• Discard any remaining bounding boxes which have an IoU greater than 0.5 with the bounding box selected as output in the previous step i.e. any bounding box with high overlap is discarded.

In case there are multiple classes/ objects, i.e., if there are four objects/classes, then non-max suppression will run four times, once for every output class.

Anchor boxes

One of the drawbacks of YOLO algorithm is that each grid can only detect one object. What if we want to detect multiple distinct objects in each grid. For example, if two objects or classes are overlapping and share the same grid as shown in the image (see Fig 4.),

We make use of anchor boxes to tackle the issue. Let’s assume the predicted variable is defined as

\begin{equation}
\hat{y} ={
\begin{bmatrix}
{p_c}& {b_x} & {b_y} & {b_h} & {b_w} & {c_1} & {c_2} & {…} & {c_8}
\end{bmatrix}}^T
\end{equation}

then, we can use two anchor boxes in the following manner to detect two objects in the image simultaneously.

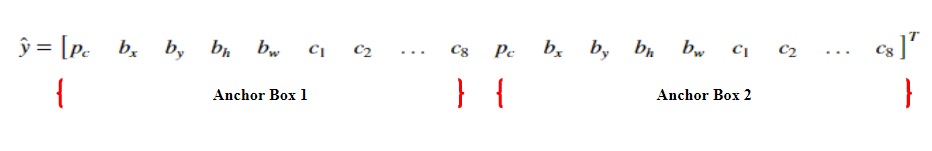
Earlier, the target variable was defined such that each object in the training image is assigned to grid cell that contains that object’s midpoint. Now, with two anchor boxes, each object in the training images is assigned to a grid cell that contains the object’s midpoint and anchor box for the grid cell with the highest IOU. So, with the help of two anchor boxes, we can detect at most two objects simultaneously in an image. Fig 6. shows the shape of the final output layer with and without the use of anchor boxes.

Although, we can detect multiple images using Anchor boxes, but they still have limitations. For example, if there are two anchor boxes defined in the target variable and the image has three overlapping objects, then the algorithm fails to detect all three objects. Secondly, if two anchor boxes are associated with two objects but have the same midpoint in the box coordinates, then the algorithm fails to differentiate between the objects. Now, that we know the basics of anchor boxes, let’s code it.

In the following code we will use 10 anchor boxes. As a result, the algorithm can detect at maximum of 10 objects in a given image.

 
def non_max_suppression(scores, classes, boxes, max_boxes=10, iou_threshold = 0.5):
    """
    Non-maximal suppression is used to fix the multiple detections of the same object.
    - Find the box_confidence (Probability of the box containing the object) for each detection.
    - Find the bounding box with the highest box_confidence
    - Suppress all the bounding boxes which have an IoU greater than 0.5 with the bounding box with the maximum box confidence.
    
    scores    -> containing the class probability score for the selected boxes.
    boxes     -> contains box coordinates for the boxes selected after threshold masking.
    classes   -> contains the index of the classes detected by the selected boxes.
    max_boxes -> maximum number of predicted boxes to be returned after NMS filtering.
    
    Returns: 
    scores  -> predicted score for each box.
    classes -> predicted class for each box.
    boxes   -> predicted box coordinates.
    """
    
    # Converting max_boxes to tensor 
    max_boxes_tensor = K.variable(max_boxes, dtype='int32')
    # Initialize the max_boxes_tensor
    K.get_session().run(tf.variables_initializer([max_boxes_tensor]))
    
    # Implement non-max suppression using tf.image.non_max_suppression()
    # tf.image.non_max_suppression() ->  Returns the indices corresponding to the boxes you want to keep
    
    indices = tf.image.non_max_suppression(boxes=boxes, scores=scores, max_output_size=max_boxes_tensor, iou_threshold=iou_threshold)
    
    # K.gather() is used to select only indices present in 'indices' variable from scores, boxes and classe
    
    scores = tf.gather(scores, indices)
    classes = tf.gather(classes, indices)
    boxes = tf.gather(boxes, indices)
    
    return scores, classes , boxes 

We can combine both the concepts threshold filtering and non-maximal suppression and apply it on the output predicted by the YOLO model. This is implemented in the code below.

 
def yolo_eval(yolo_outputs, image_shape = (720., 1280.), max_boxes = 10, score_threshold = 0.6, iou_threshold = 0.5):
    """
    The function takes the output of the YOLO encoding/ model and filters the boxes using 
    score threshold and non-maximal suppression. Returns the predicted boxes along with their scores,
    box coordinates and classes.
    
    Arguments: 
    yolo_outputs    -> Output of the encoding model. 
    image_shape     -> Input shape 
    max_boxes       -> Maximum number of predicted boxes to be returned after NMS filtering.
    score_threshold -> Threshold value for box class score, if the maximum class probability score < threshold,
                       then discard that box. 
    iou_threshold   -> 'Intersection over Union' threshold used for NMS filtering
    
    Returns: 
    scores  -> predicted score for each box.
    classes -> predicted class for each box.
    boxes   -> predicted box coordinates.
    """
    
    box_xy, box_wh, box_confidence, box_class_probs = yolo_outputs
    
    # Convert boxes to be ready for filtering functions
    boxes = yolo_boxes_to_corners(box_xy, box_wh)
    
    scores, classes, boxes = yolo_filter_boxes(box_confidence, boxes, box_class_probs, score_threshold)
    
    # Scale boxes back to original image shape.
    boxes = scale_boxes(boxes, image_shape)
    
    # Perform non-max suppression
    scores, classes , boxes = non_max_suppression(scores, classes, boxes, max_boxes, iou_threshold)
    
    return scores, boxes, classes

Object Detection on Sample Test Image

We will use the trained model to predict the respective classes and the corresponding bounding boxes on a sample of images. The function ‘draw’ runs a tensorflow session and calculates the confidence scores, bounding box coordinates and the output class probabilities for the given sample image. Finally, it computes the x_min, x_max, y_min, y_max from b_x,b_y,b_w,b_h, scales the bounding boxes according to the input sample image and draws the bounding boxes and class probability for the objects in the input sample image.

 
# Loading the path of the test image data
test = glob('data/test/*.jpg')
# Reading and storing the test image data
test_data = []
for i in test:
    test_data.append(plt.imread(i))
# Processing the test image data 
test_data = process_data(test_data)

# Predicting the scores, boxes, classes for the given input image
scores, boxes, classes, model_body, input_image_shape = load_yolo(model_body, class_names, anchors)
# Drawing the bounding boxes
draw(model_body, scores, boxes, classes,input_image_shape, test_data, image_set='all', out_path='data/test/output/',save_all=False)

Fig. 7, shows the class probabilities and bounding boxes on the test images.

Implementing the Model on Real Time Video

Next, we will implement the model on a real time video. Since, video is a sequence of images at different time frames, so we will predict the class probabilities and bounding boxes for the image captured at each time frame. We will use OpenCV video capture function to read the video and convert it into image/ frames at different time steps. The video below demonstrates the implementation of the algorithm on a real time video.

 
#Path of the stored video file
videopath = 'data/real_time/bdd-videos-sample.mp4'

# Loads the saved trained YOLO model
scores, boxes, classes, model_body, input_image_shape = load_yolo(model_body, class_names, anchors)

# Catures and splits the video into images at different time frames 
vc = cv2.VideoCapture(videopath)

 
while(True):
    # Load the image at each time frame
    check, frame = vc.read()
    # Preprocess the input image frame
    frame = process_data(np.expand_dims(frame, axis=0))
    # Predict and draw the class probabilities and bounding boxes for the given frame
    img_data = draw(model_body, scores, boxes, classes, input_image_shape, frame, image_set='real', save_all=False, real_time=True)
    img_data = np.array(img_data)
    # Display the image/ frame with the predicted class probability and bounding boxes back on the screen.
    cv2.imshow('Capture:', img_data)
    key = cv2.waitKey(1)
    if key == ord('q'):
        break
vc.release()
cv2.destroyAllWindows() 

[Source Code]

Conclusion

This brings us to the end of this article. Congratulate yourself on reaching to the end of this blog. As a reward you now have a better understanding of how object detection works (using the YOLO algorithm) and how self driving cars implement this technique to differentiate between cars, trucks, pedestrians, etc. to make better decisions. Finally, I encourage you to implement and play with the code yourself. You can find the full source code related to this article here.

Have anything to say? Feel free to comment below for any questions, suggestions, and discussions related to this article. Till then, keep hacking with HackerEarth.

Struggling to compose your own music, check out this blog on how to Compose Jazz Music with Deep Learning.

References

• DarkNet (YOLOv2)  https://pjreddie.com/darknet/yolov2/
• You Only Look Once: Unified, Real-Time Object Detection – Joseph Redmon, Santosh Divvala, Ross Girshick, Ali Farhadi. arXiv:1612.08242 [cs.CV]
• YAD2K: Yet Another Darknet 2 Keras – Allan Zelener : https://github.com/allanzelener/YAD2K
• Berkley Deep Driving Dataset : http://bdd-data.berkeley.edu/

Shubham Gupta Author 6 Blogs