Minimax Algorithm with Alpha-beta pruning

Ever since the advent of Artificial Intelligence (AI), game playing has been one of the most interesting applications of AI.

The first chess programs were written by Claude Shannon and by Alan Turing in 1950, almost as soon as the computers became programmable.

Games such as chess, tic-tac-toe, and Go are interesting because they offer a pure abstraction of the competition between the two armies.

It is this abstraction which makes game playing an attractive area for AI research.

In this article, we will go through the basics of the Minimax algorithm along with the functioning of the algorithm.

We will also take a look at the optimization of the minimax algorithm, alpha-beta pruning.

What is the Minimax algorithm?

Minimax is a recursive algorithm which is used to choose an optimal move for a player assuming that the other player is also playing optimally.

It is used in games such as tic-tac-toe, go, chess, Isola, checkers, and many other two-player games.

Such games are called games of perfect information because it is possible to see all the possible moves of a particular game.

There can be two-player games which are not of perfect information such as Scrabble because the opponent’s move cannot be predicted.

It is similar to how we think when we play a game: “if I make this move, then my opponent can only make only these moves,” and so on.

Minimax is called so because it helps in minimizing the loss when the other player chooses the strategy having the maximum loss.

Terminology

• Game Tree: It is a structure in the form of a tree consisting of all the possible moves which allow you to move from a state of the game to the next state.

A game can be defined as a search problem with the following components:

• Initial state: It comprises the position of the board and showing whose move it is.
• Successor function: It defines what the legal moves a player can make are.
• Terminal state: It is the position of the board when the game gets over.
• Utility function: It is a function which assigns a numeric value for the outcome of a game. For instance, in chess or tic-tac-toe, the outcome is either a win, a loss, or a draw, and these can be represented by the values +1, -1, or 0, respectively. There are games that have a much larger range of possible outcomes; for instance, the utilities in backgammon varies from +192 to -192. A utility function can also be called a payoff function.

Further Reading

Would you like to get updates once a month on our latest articles? We won't spam, we promise. Subscribe now to The HackerEarth Blog!

How does the algorithm work?

There are two players involved in a game, called MIN and MAX. The player MAX tries to get the highest possible score and MIN tries to get the lowest possible score, i.e., MIN and MAX try to act opposite of each other.

The general process of the Minimax algorithm is as follows:

Step 1: First, generate the entire game tree starting with the current position of the game all the way upto the terminal states. This is how the game tree looks like for the game tic-tac-toe.

Let us understand the defined terminology in terms of the diagram above.

1. The initial state is the first layer that defines that the board is blank it’s MAX’s turn to play.
2. Successor function lists all the possible successor moves. It is defined for all the layers in the tree.
3. Terminal State is the last layer of the tree that shows the final state, i.e whether the player MAX wins, loses, or ties with the opponent.
4. Utilities in this case for the terminal states are 1, 0, and -1 as discussed earlier, and they can be used to determine the utilities of the other nodes as well.

Step 2: Apply the utility function to get the utility values for all the terminal states.
Step 3: Determine the utilities of the higher nodes with the help of the utilities of the terminal nodes. For instance, in the diagram below, we have the utilities for the terminal states written in the squares.

Let us calculate the utility for the left node(red) of the layer above the terminal. Since it is the move of the player MIN, we will choose the minimum of all the utilities. For this case, we have to evaluate MIN{3, 5, 10}, which we know is certainly 3. So the utility for the red node is 3.

Similarly, for the green node in the same layer, we will have to evaluate MIN{2,2} which is 2.

Step 4: Calculate the utility values with the help of leaves considering one layer at a time until the root of the tree.
Step 5: Eventually, all the backed-up values reach to the root of the tree, i.e., the topmost point. At that point, MAX has to choose the highest value.

In our example, we only have 3 layers so we immediately reached to the root but in actual games, there will be many more layers and nodes. So we have to evaluate MAX{3,2} which is 3.

Therefore, the best opening move for MAX is the left node(or the red one). This move is called the minimax decision as it maximizes the utility following the assumption that the opponent is also playing optimally to minimize it.

To summarize,

Minimax Decision = MAX{MIN{3,5,10},MIN{2,2}}
= MAX{3,2}
= 3

Psuedocode:

function minimax(node, depth, maximizingPlayer)
            if depth = 0 or node is a terminal node
                   return the utility of the node

            if maximizingPlayer
                   bestValue := ??
            for each child of node
                   v := minimax(child, depth ? 1, FALSE)
                   bestValue := max(bestValue, v)
            return bestValue  

            else (* minimizing player *)
                   bestValue := +?
                   for each child of node
                          v := minimax(child, depth ? 1, TRUE)
                          bestValue := min(bestValue, v)
                   return bestValue

Optimization

Game trees are, in general, very time consuming to build, and it’s only for simple games that it can be generated in a short time.

If there are \(b\) legal moves, i.e., \(b\) nodes at each point and the maximum depth of the tree is \(m\), the time complexity of the minimax algorithm is of the order \(b^m (O(b^m))\).

To curb this situation, there are a few optimizations that can be added to the algorithm.

Fortunately, it is viable to find the actual minimax decision without even looking at every node of the game tree. Hence, we eliminate nodes from the tree without analyzing, and this process is called pruning.

Alpha-beta pruning

The method that we are going to look in this article is called alpha-beta pruning.

If we apply alpha-beta pruning to a standard minimax algorithm, it returns the same move as the standard one, but it removes (prunes) all the nodes that are possibly not affecting the final decision.

Let us understand the intuition behind this first and then we will formalize the algorithm. Suppose, we have the following game tree:

In this case,
Minimax Decision = MAX{MIN{3,5,10}, MIN{2,a,b}, MIN{2,7,3}}
= MAX{3,c,2}
= 3

You would be surprised!

How could we calculate the maximum with a missing value? Here is the trick. MIN{2,a,b} would certainly be less than or equal to 2, i.e., c<=2 and hence MAX{3,c,2} has to be 3.

The question now is do we really need to calculate c? Of course not.

We could have reached a conclusion without looking at those nodes. And this is where alpha-beta pruning comes into the picture.

A few definitions:

Alpha: It is the best choice so far for the player MAX. We want to get the highest possible value here.
Beta: It is the best choice so far for MIN, and it has to be the lowest possible value.

Note: Each node has to keep track of its alpha and beta values. Alpha can be updated only when it’s MAX’s turn and, similarly, beta can be updated only when it’s MIN’s chance.

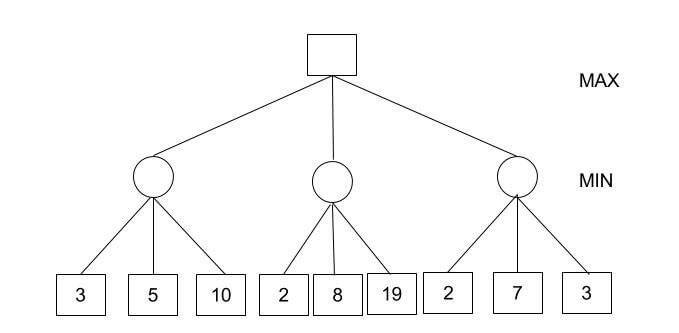
How does alpha-beta pruning work?

1. Initialize alpha = -infinity and beta = infinity as the worst possible cases. The condition to prune a node is when alpha becomes greater than or equal to beta.
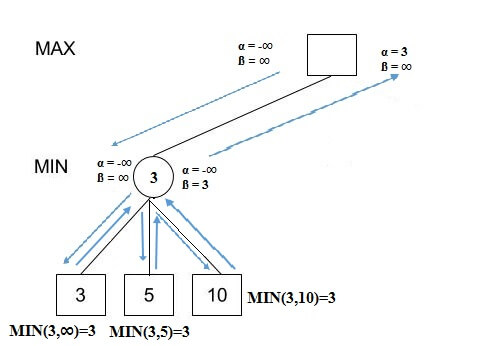
2. Start with assigning the initial values of alpha and beta to root and since alpha is less than beta we don’t prune it.
3. Carry these values of alpha and beta to the child node on the left. And now from the utility value of the terminal state, we will update the values of alpha and be, so we don’t have to update the value of beta. Again, we don’t prune because the condition remains the same. Similarly, the third child node also. And then backtracking to the root we set alpha=3 because that is the minimum value that alpha can have.
   
4. Now, alpha=3 and beta=infinity at the root. So, we don’t prune. Carrying this to the center node, and calculating MIN{2, infinity}, we get alpha=3 and beta=2.
5. Prune the second and third child nodes because alpha is now greater than beta.
6. Alpha at the root remains 3 because it is greater than 2. Carrying this to the rightmost child node, evaluate MIN{infinity,2}=2. Update beta to 2 and alpha remains 3.
7. Prune the second and third child nodes because alpha is now greater than beta.
8. Hence, we get 3, 2, 2 at the left, center, and right MIN nodes, respectively. And calculating MAX{3,2,2}, we get 3. Therefore, without even looking at four leaves we could correctly find the minimax decision.

Pseudocode (Source: NPTEL Course):

evaluate (node, alpha, beta)
     if node is a leaf
        return the utility value of node
     if node is a minimizing node
        for each child of node
            beta = min (beta, evaluate (child, alpha, beta))
            if beta <= alpha
                return beta
            return beta
     if node is a maximizing node
        for each child of node
            alpha = max (alpha, evaluate (child, alpha, beta))
            if beta <= alpha
                return alpha
            return alpha

Conclusion

Games are very appealing and writing game-playing programs is perhaps even more exciting. What Grand Prix racing is to the car industry, game playing is to AI.

Just as we would not expect a racing car to run perfectly on a bumpy road, we should not expect game playing algorithms to be perfect for every situation.

So is the minimax algorithm. It may not be the best solution to all kinds of computer games that need to have AI.

But given a good implementation, it can create a tough competitor.

Rashmi Jain Author 17 Blogs