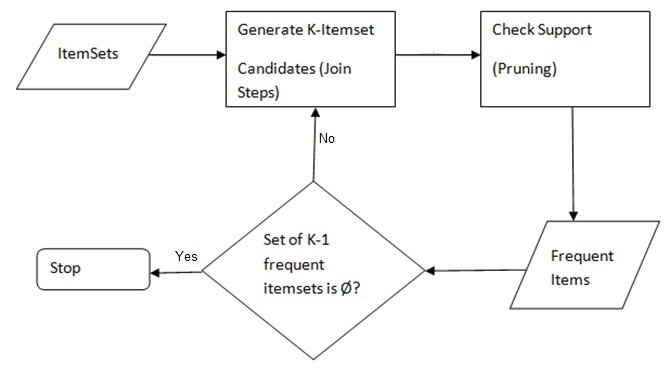
Now that we have looked at an example of the functionality of Apriori Algorithm, let us formulate the general process.
General Process of the Apriori algorithm
The entire algorithm can be divided into two steps:
Step 1: Apply minimum support to find all the frequent sets with k items in a database.
Step 2: Use the self-join rule to find the frequent sets with k+1 items with the help of frequent k-itemsets. Repeat this process from k=1 to the point when we are unable to apply the self-join rule.
This approach of extending a frequent itemset one at a time is called the “bottom up” approach.
Mining Association Rules
Till now, we have looked at the Apriori algorithm with respect to frequent itemset generation. There is another task for which we can use this algorithm, i.e., finding association rules efficiently.
For finding association rules, we need to find all rules having support greater than the threshold support and confidence greater than the threshold confidence.
But, how do we find these? One possible way is brute force, i.e., to list all the possible association rules and calculate the support and confidence for each rule. Then eliminate the rules that fail the threshold support and confidence. But it is computationally very heavy and prohibitive as the number of all the possible association rules increase exponentially with the number of items.
Given there are n items in the set [latex]I[/latex], the total number of possible association rules is [latex]3^n - 2^{n+1} + 1[/latex].
We can also use another way, which is called the two-step approach, to find the efficient association rules.
The two-step approach is:
Step 1: Frequent itemset generation: Find all itemsets for which the support is greater than the threshold support following the process we have already seen earlier in this article.
Step 2: Rule generation: Create rules from each frequent itemset using the binary partition of frequent itemsets and look for the ones with high confidence. These rules are called candidate rules.
Let us look at our previous example to get an efficient association rule. We found that OPB was the frequent itemset. So for this problem, step 1 is already done. So, let’ see step 2. All the possible rules using OPB are:
OP[latex]\longrightarrow[/latex]B, OB[latex]\longrightarrow[/latex]P, PB[latex]\longrightarrow[/latex]O, B[latex]\longrightarrow[/latex] OP, P[latex]\longrightarrow[/latex]OB, O[latex]\longrightarrow[/latex]PBIf [latex]X[/latex] is a frequent itemset with k elements, then there are [latex]2^k-2[/latex] candidate association rules.We will not go deeper into the theory of the Apriori algorithm for rule generation.Pros of the Apriori algorithm
- It is an easy-to-implement and easy-to-understand algorithm.
- It can be used on large itemsets.
Cons of the Apriori Algorithm
- Sometimes, it may need to find a large number of candidate rules which can be computationally expensive.
- Calculating support is also expensive because it has to go through the entire database.
R implementation
The package which is used to implement the Apriori algorithm in R is called arules. The function that we will demonstrate here which can be used for mining association rules is
apriori(data, parameter = NULL)
The arguments of the function apriori are
data: The data structure which can be coerced into transactions (e.g., a binary matrix or data.frame).
parameter: It is a named list containing the threshold values for support and confidence. The default value of this argument is a list of minimum support of 0.1, minimum confidence of 0.8, maximum of 10 items (maxlen), and a maximal time for subset checking of 5 seconds (maxtime).
https://gist.github.com/HackerEarthBlog/98dca27a7e48694506db6ae413d7570e