Sometimes, there are more than one way to solve a problem. We need to learn how to compare the performance different algorithms and choose the best one to solve a particular problem. While analyzing an algorithm, we mostly consider time complexity and space complexity. Time complexity of an algorithm quantifies the amount of time taken by an algorithm to run as a function of the length of the input. Similarly, Space complexity of an algorithm quantifies the amount of space or memory taken by an algorithm to run as a function of the length of the input.
Time and space complexity depends on lots of things like hardware, operating system, processors, etc. However, we don't consider any of these factors while analyzing the algorithm. We will only consider the execution time of an algorithm.
Lets start with a simple example. Suppose you are given an array $$A$$ and an integer $$x$$ and you have to find if $$x$$ exists in array $$A$$.
Simple solution to this problem is traverse the whole array $$A$$ and check if the any element is equal to $$x$$.
for i : 1 to length of A
if A[i] is equal to x
return TRUE
return FALSE
Each of the operation in computer take approximately constant time. Let each operation takes $$c$$ time. The number of lines of code executed is actually depends on the value of $$x$$. During analyses of algorithm, mostly we will consider worst case scenario, i.e., when $$x$$ is not present in the array $$A$$. In the worst case, the if condition will run $$N$$ times where $$N$$ is the length of the array $$A$$. So in the worst case, total execution time will be $$(N * c + c)$$. $$N * c$$ for the if condition and $$c$$ for the return statement ( ignoring some operations like assignment of $$i$$ ).
As we can see that the total time depends on the length of the array $$A$$. If the length of the array will increase the time of execution will also increase.
Order of growth is how the time of execution depends on the length of the input. In the above example, we can clearly see that the time of execution is linearly depends on the length of the array. Order of growth will help us to compute the running time with ease. We will ignore the lower order terms, since the lower order terms are relatively insignificant for large input. We use different notation to describe limiting behavior of a function.
$$O$$-notation:
To denote asymptotic upper bound, we use $$O$$-notation. For a given function $$g(n)$$, we denote by $$O(g(n))$$ (pronounced “big-oh of g of n”) the set of functions:
$$O(g(n)) =$$ { $$f(n)$$ : there exist positive constants $$c$$ and $$n_0$$ such that $$0 \le f (n) \le c * g(n)$$ for all $$n \ge n_0$$ }
$$\Omega$$-notation:
To denote asymptotic lower bound, we use $$\Omega$$-notation. For a given function $$g(n)$$, we denote by $$\Omega(g(n))$$ (pronounced “big-omega of g of n”) the set of functions:
$$\Omega(g(n)) =$$ { $$f(n)$$ : there exist positive constants $$c$$ and $$n_0$$ such that $$0 \le c * g(n) \le f(n)$$ for all $$n \ge n_0$$ }
$$\Theta$$-notation:
To denote asymptotic tight bound, we use $$\Theta$$-notation. For a given function $$g(n)$$, we denote by $$\Theta(g(n))$$ (pronounced “big-theta of g of n”) the set of functions:
$$\Theta(g(n)) =$$ { $$f (n)$$ : there exist positive constants $$c_1,\;c_2$$ and $$n_0$$ such that $$0 \le c_1 * g(n) \le f (n) \le c_2 * g(n)$$ for all $$n \gt n_0$$ }
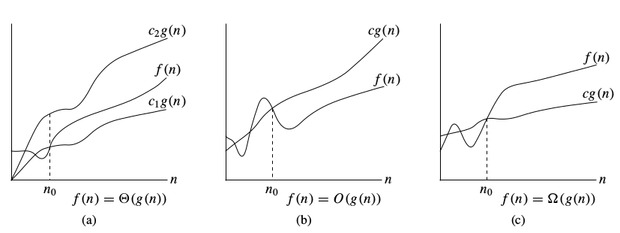
Time complexity notations
While analysing an algorithm, we mostly consider $$O$$-notation because it will give us an upper limit of the execution time i.e. the execution time in the worst case.
To compute $$O$$-notation we will ignore the lower order terms, since the lower order terms are relatively insignificant for large input.
Let $$f(N) = 2 * N^2 + 3 * N + 5$$
$$O(f(N)) = O(2 * N^2 + 3 * N + 5) = O(N^2)$$
Lets consider some example:
1.
int count = 0;
for (int i = 0; i < N; i++)
for (int j = 0; j < i; j++)
count++;
Lets see how many times count++ will run.
When $$i = 0$$, it will run $$0$$ times.
When $$i = 1$$, it will run $$1$$ times.
When $$i = 2$$, it will run $$2$$ times and so on.
Total number of times count++ will run is $$0 + 1 + 2 + ... + (N-1) = \frac{N * (N-1)}{2}$$. So the time complexity will be $$O(N^2)$$.
2.
int count = 0;
for (int i = N; i > 0; i /= 2)
for (int j = 0; j < i; j++)
count++;
Think about how many times count++ will run.
When $$i = N$$, it will run $$N$$ times.
When $$i = N / 2$$, it will run $$N / 2$$ times.
When $$i = N / 4$$, it will run $$N / 4$$ times and so on.
Total number of times count++ will run is $$N + N / 2 + N / 4 + ... + 1 = 2 * N$$. So the time complexity will be $$O(N)$$.
The table below is to help you understand the growth of several common time complexities, and thus help you judge if your algorithm is fast enough to get an Accepted ( assuming the algorithm is correct ).
| Length of Input (N) | Worst Accepted Algorithm |
|---|---|
| $$\le [10..11]$$ | $$O(N!), O(N^6)$$ |
| $$\le [15..18]$$ | $$O(2^N * N^2)$$ |
| $$\le [18..22]$$ | $$O(2^N * N)$$ |
| $$\le 100$$ | $$O(N^4)$$ |
| $$\le 400$$ | $$O(N^3)$$ |
| $$\le 2K$$ | $$O(N^2 * logN)$$ |
| $$\le 10K$$ | $$O(N^2)$$ |
| $$\le 1M$$ | $$O(N * logN)$$ |
| $$\le 100M$$ | $$O(N), O(logN), O(1)$$ |

