Three friends Navneet, Gaurav and Rishab want to play with a frisbee. As its a rainy season the ground is wet and muddy. So, Navneet picked N good spots (with integer coordinates) where each of them can stand and play (one person on one spot).
Gaurav being a great Mathematician wants to know the maximum possible area of a triangle that can be formed from those N spots, such that each of the three vertices of that triangle must be a part of at least one right-angled-triangle formed from those N spots. As he is busy playing frisbee so, he asked you for help. Note that those three vertices may be a part of same or different right-angled-triangles (i.e. if △ABC is the triangle with the maximum area then vertices A,B,C must be a part of atleast one right-triangle but it is not compulsory that they must be a part of same right-triangle and △ABC may or may not be a right-triangle).
It is guaranteed that the solution exists.
Input:
First line contains the integer N.
Each of the next N lines contains two space-seperated integers x, y
denoting the point (x,y)
Constraints:
1≤N≤20001≤x≤41≤y≤109
Output:
If P is you answer then output a single line containing the number 2*P.
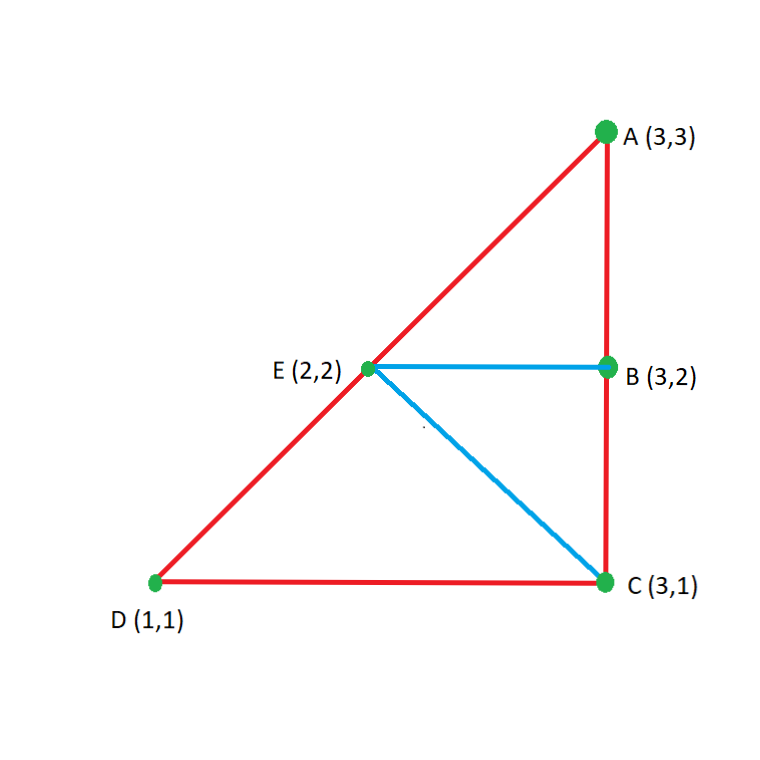
From the above figure:-
Point (1,1) is a part of right-triangles DEC and DCA.
Point (2,2) is a part of right-triangles DEC, EBA, EBC and AEC.
Point (3,3) is a part of right-triangles DEC and EBA.
Point (3,1) is a part of right-triangles CBE, DEC and DCA.
Point (3,2) is a part of right-triangles CBE and EBA.
Here all the points are part of atleast one right-triangle and triangle ACD has the maximum area i.e. 2 sq units. So, the required answer is 2*2 = 4.

