Jaggu monkey is a master tree climber. But now he is bored of climbing simple trees. Since all his friends are angry with him because of his annyoing activities. So, he asked Doraemon to help. Doraemon didn't disappoint him. He showed him a gadget called Anti-binary tree.
An anti-binary tree is a rooted and weighted tree having n nodes numbered from 1 to n, node 1 is the root node. All its nodes except the nodes of ultimate (last) and possibly penultimate level (2nd last level), have two or more children.
Formally, if the height of the tree is H, then their is no limitation on nodes at depth H and H-1, for other nodes, the number of its children has to be two or more than two.
A tree is an undirected and connected graph with n nodes and n-1 edges.
Given tree is flexible. Initially, length of ith edge is wi but later it may increase.
Doraemon will give this tree to Jaggu if he answers his q queries
There are two types of queries
-
0 a b (a!=b)
- 1 a b c (a!=b)
For type 1 queries- he needs to find the length of the simple path from a to b.
For type 2 queries- It is an update query. It denotes that length of all edges in the simple path from a to b gets increased by c.
Jaggu doesn't know graph theory so he asked you to help.
Being Mr. Programmer help him to answer the queries.
Input format:
- First line contains a single integer t denoting number of test cases.
- 1st line of each test case contains two space seperated integers n and q denoting number of nodes and number of queries respectively.
- Next n-1 line contains three space seperated integers u, v and w denoting an edge between u and v with weight w.
- Next q lines contains q queries.
Output format:
- For type 1 queries, print a single integer in new line.
Constraints:
1<=t<=20000
1<=n,q<=105
1<=u,v,a,b<=n,u!=v
1<=w,c<=109
Sum of n or q over all test cases doesn't exceed 2*105.
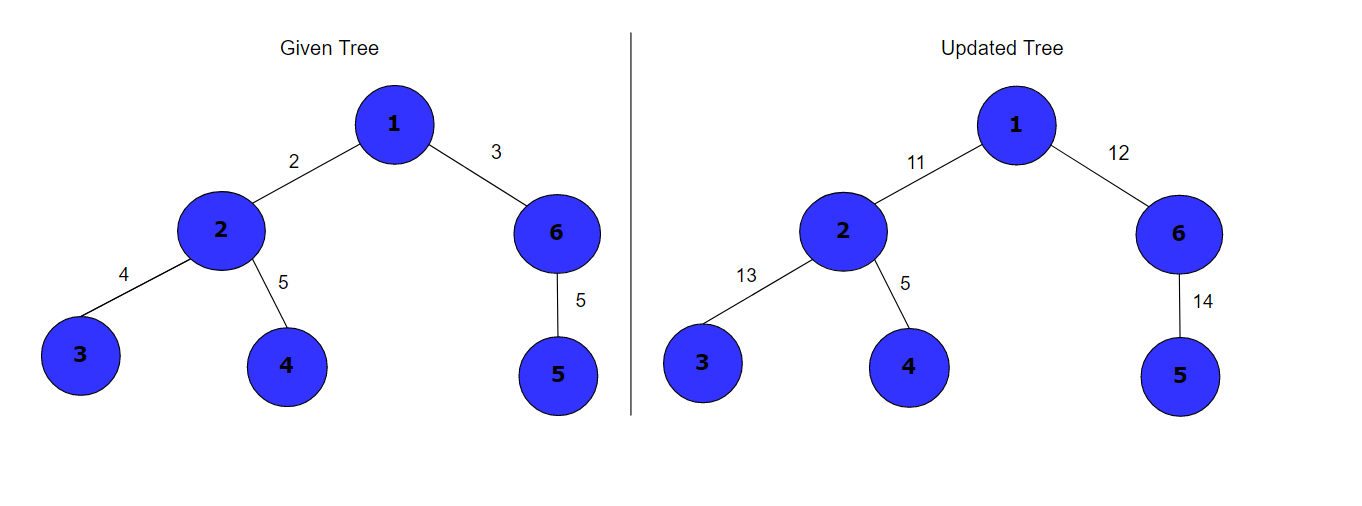
In updated tree, length of path from node 2 to node 6 = 11+12 = 23

