Childhood is the most memorable phase of our life. So this question is based on one  of the many such memories.

There is school where N children study. There are N gates in the school, using which children get in and out of the school. All gates are arranged in a single row. After the gates, there is big field, beyond which is a Parking Lot with N positions marked.

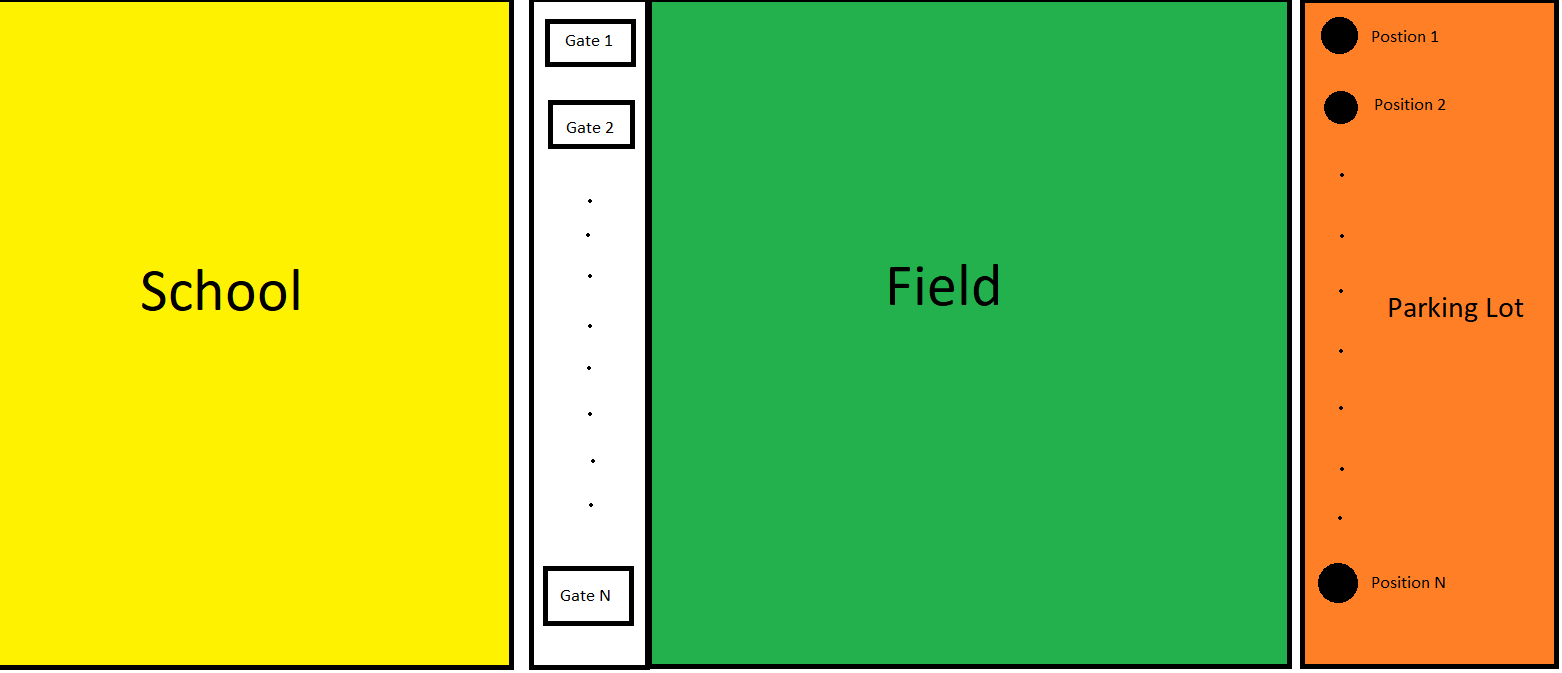
Each child has a designated gate, that he/she uses which is fixed. When the school gets over, the father of every child comes to receive him/her and waits in the Parking Lot in a previously fixed position. So the every child has a fixed gate from where he/she will come out and his/her father will wait at a fixed position in the Parking Lot. No 2 children will have the same father.

After coming out of the gates, the children run to their respective fathers. In doing so, their paths may intersect, in which case both of them shout "YEAH" (this activity takes 0 time). So given the information about the gate a child comes out and where his/her father is in the Parking Lot, can you answer how many MAXIMUM  number of times "YEAH" will be uttered.

CONDITION:

1. No 2 child can intersect their path more than once.

2. Children don't need to run along the shortest path from the gate to their father.

3. The X component of the velocity of every child at any point of time is same for all children, i.e., a child cannot run faster than any body else along the field.

Input:

The first line contains T, the number of testcases.

The first line of each testcase contains N, the number of children.

The second line of each testcase contains N integers, i'th number denoting the gate number of the i'th child.

The third line of each testcase contains N integers, i'th number denoting the location of parent of the i'th child.

Output:

The answer to each testcase in a new line.

Constraints:

1<=T<=10

1<=N<=100000

1<=Gate[i]<=N

1<=Father[i]<=N

Problem Setter : Aditya Ghosh