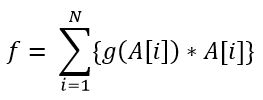Chotu is going to a birthday party tonight!!!
Obviously, he was too happy about it, but he was informed about the surprise lab test by Rahul Kala Sir. And to make it worse, the timings for the lab test is 5:00 PM and the bus for civil lines leaves at 6:00 PM. So, he needs to be quick at solving lab test problem in order to catch bus in time.
So he asks you, his best programmer friend for help.
You are given a list A constructed from a full binary tree containing N nodes in following manner.
fun genList(x) returns list A
if(x->left_child == null && x->right_child == null)
return []
list p = []
p.append(genList(x->left_child))
p.append(x)
p.append(genList(x->right_child))
return p
The value of a function g(x) can be calulated by following code snippet.
fun g(x) returns integer
if(x->left_child == null && x->right_child == null)
return 1;
else
return max(g(x->left_child) + 1, g(x->right_child) + 1)
Now he has been asked to print the value of following function
Can you help him get to birthday party in time?
Input
First line contains a single integer T denoting number of test cases.
First line of each test case contains a integer N denoting number of nodes in full binary tree.
Second line of each test case contains N space separated integers denoting the List A.
Output
Print T lines, each containing a single integer, value of function f for that test case.
Constraints
1 <= T <= 100
1 <= N <= 105
1 <= Ai <= 100
Note
1 - Every node of a full binary tree except leaf, has 2 children and the last level of the tree is completely filled.
2 - Large I/O files, use scanf/printf instead of cin/cout.
3 - Given tree is guaranteed to be a full binary tree.
Following is the tree for given sample case.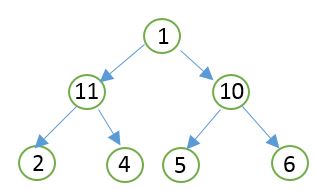
Now the value of g(x) for all nodes will be-
g(1) = 3
g(11) = 2
g(10) = 2
g(2) = 1
g(4) = 1
g(5) = 1
g(6) = 1
Value of function f will be {g(1) * 1} + {g(11) * 11} + {g(10) * 10} + {g(2) * 2} + {g(4) * 4} + {g(5) * 5} + {g(6) * 6} = 62.