Definition :

A linear recurrence relation is a function or a sequence such that each term is a linear combination of previous terms. Each term can be described as a function of the previous terms.

A famous example is the Fibonacci sequence: f(i) = f(i-1) + f(i-2)

Linear means that the previous terms in the definition are only multiplied by a constant (possibly zero) and nothing else. So, this sequence f(i) = f(i-1) * f(i-2) is not a linear recurrence.

Problem

Given a function f(x) defined as a linear recurrence relation. Compute f(N) ,where N is a large number .

Solution

The solution is broken down into 4 steps :

1. Determine K , the number of terms on which f(i) depends
   
   K is the minimum integer such that f(i) doesn’t depend on f(i-M), for all M > K.
   For Fibonacci sequence, because the relation is
   
   
   
   therefore, K = 2.
   
   
2. Determine vector F₁, the initial values
   
   If each term of a recurrence relation depends on K previous terms, then it must have the first K terms defined, otherwise the whole sequence is undefined. For Fibonacci sequence (K = 2), the well-known initial values are:
   
   f(1)=1 , f(2)=1
   
   We define a column vector F_i as a K x 1 matrix whose first row is f(i), second row is f(i+1), and so on, until K^th row is f(i+K-1). The initial values of f are given in column vector F₁ that has values f(1) through f(K):
   
   
   
   
3. Determine T, the transformation matrix
   
   This is the most important step in solving recurrence relation. The heart of this method is to construct a K x K matrix T, called transformation matrix, such that
   
   
   
   Here is how to construct it. Suppose that
   
   .
   
   You can solve this equation with any method, and obtain the result:
   
   
   
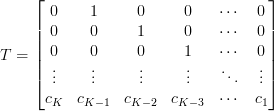
   More precisely, T is a K x K matrix whose last row is a vector
   
   
   
   , and for the other rows, the i^th row is a zero vector except that its (i+1)^th element is 1.
   
   Let’s apply it to our example. In Fibonacci sequence,
   
   
   
   
4. Determine F_N
   
   After we construct the transformation matrix, the rest is very simple. We can obtain F_i for any i, by repeatedly multiplying T with F₁. For example, to obtain F₂,
   
   
   
   To obtain F₃,
   
   
   
   And so on. In general,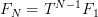
   
   
   
   Therefore, the original problem is now (almost) solved: compute F_N as above, and then we can obtain f(N): it is exactly the first row of F_N. In case of our Fibonacci sequence, the N^th term in Fibonacci sequence is the first row of:
   
   
   
   

What remains is how to compute T^N-1 efficiently. The most popular method is to use exponentiation by squaring method that works in O(log N) time, with this recurrence:

Multiplying two matrices takes O(K³) time using standard method, so the overall time complexity to solve a linear recurrence is O(K³ log N).

Here is a sample C++ code to compute the N-th term of Fibonacci sequence, modulo 1,000,000,007.

#include<iostream>
#include<vector>
#define REP(i,n) for (int i = 1; i &lt;= n; i++)
using namespace std;

typedef long long ll;
typedef vector<vector<ll> > matrix;
const ll MOD = 1000000007;
const int K = 2;

// computes A * B
matrix mul(matrix A, matrix B)
{
    matrix C(K+1, vector<ll>(K+1));
    REP(i, K) REP(j, K) REP(k, K)
        C[i][j] = (C[i][j] + A[i][k] * B[k][j]) % MOD;
    return C;
}

// computes A ^ p
matrix pow(matrix A, int p)
{
    if (p == 1)
        return A;
    if (p % 2)
        return mul(A, pow(A, p-1));
    matrix X = pow(A, p/2);
    return mul(X, X);
}

// returns the N-th term of Fibonacci sequence
int fib(int N)
{
    // create vector F1
    vector<ll> F1(K+1);
    F1[1] = 1;
    F1[2] = 1;

    // create matrix T
     matrix T(K+1, vector<ll>(K+1));
     T[1][1] = 0, T[1][2] = 1;
     T[2][1] = 1, T[2][2] = 1;

     // raise T to the (N-1)th power
     if (N == 1)
         return 1;
     T = pow(T, N-1);

         // the answer is the first row of T . F1
     ll res = 0;
     REP(i, K)
         res = (res + T[1][i] * F1[i]) % MOD;
    return res;
}