Introduction To Dynamic Programming
DP is a very useful and effective technique for finding optimal solution for problems having exponential time complexities( O(n!) or O(2^n) ) as it may bring down the complexity to O(n^2) or O(n^3).
DP applies to the problems having overlapping sub-problems.DP computes sub-problems before the problem itself and combines value of sub-problem to generate solution to the problem. Since problems are overlapping we may end up computing same sub-problems over and over again.So, DP speeds up the process by storing those results in a table and fetch result instead of computing it again.
For ex :
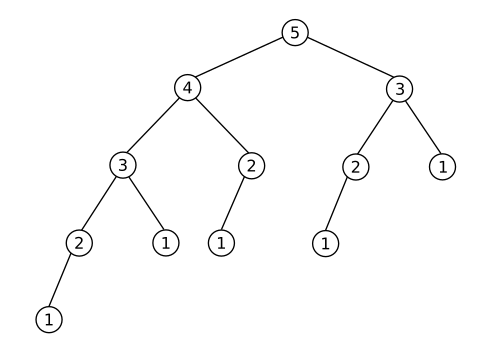
Take an example of Fibonacci series, fibo(4) and fibo(3) are sub-problems to fibo(5) and as we can see from image we'll compute fibo(3) twice one while computing fibo(5) and one while computing fibo(4), that's a lot of wastage, in DP technique we'll store fibo(3) and use this result when required.
Let's take a simple example: Problem: Given an array of integers of size n.We've to answer Q queries.Each query consists of 2 integers L and R and we've to print sum of elements of array from L to R(inclusive).
input: 5 1 2 3 4 5 2 1 5 2 5 output: 15 14
Naive: For each query iterate through L to R and calculate the sum
for q<-1 upto Q:
sum = 0
for i<-L upto R:
sum = sum + Arr[i]
print sum
.:for single Query takes O(n) time and for answering Q queries it takes O(Q*n) time.
DP : Find and store the cumulative frequency in a table(array)
table[1...n] = {0}
table[0] = Arr[0]
for i<-1 upto n:
table[i] = table[i-1] + Arr[i]
this pre-computation requires O(n) time. Now we can answer each query in O(1) time as follows:
for q<-1 upto Q:
print (table[R] - table[L-1])
.: for Q queries complexity becomes O(1*Q) = O(Q)
So, overall complexity of problem using DP is: O(Q+n) which is linear in time. Though DP requires Extra space of order O(n), but the reduction in the time complexity covers for it.
Exercise: Write an algorithm to compute Fibonacci series using DP.
The implementation of fibonacci series in Python using both Top down and Bottom approach can be found at - https://youtu.be/OEtW3Fmmrpk
