Heaps/Priority Queues

Heaps

A heap is a tree-based data structure in which all the nodes of the tree are in a specific order.

For example, if $$X$$ is the parent node of $$Y$$, then the value of $$X$$ follows a specific order with respect to the value of $$Y$$ and the same order will be followed across the tree.

The maximum number of children of a node in a heap depends on the type of heap. However, in the more commonly-used heap type, there are at most $$2$$ children of a node and it's known as a Binary heap.

In binary heap, if the heap is a complete binary tree with $$N$$ nodes, then it has smallest possible height which is $$log_2N$$ .

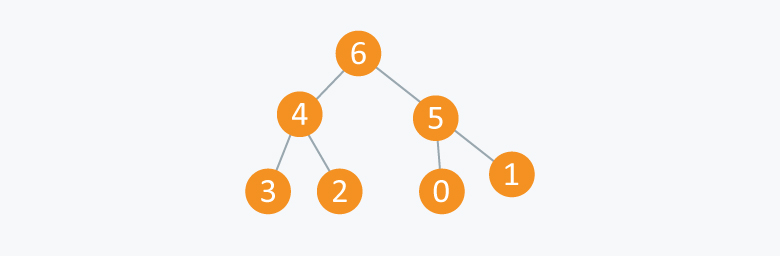
In the diagram above, you can observe a particular sequence, i.e each node has greater value than any of its children.

Suppose there are $$N$$ Jobs in a queue to be done, and each job has its own priority. The job with maximum priority will get completed first than others. At each instant, we are completing a job with maximum priority and at the same time we are also interested in inserting a new job in the queue with its own priority.

So at each instant we have to check for the job with maximum priority to complete it and also insert if there is a new job. This task can be very easily executed using a heap by considering $$N$$ jobs as $$N$$ nodes of the tree.

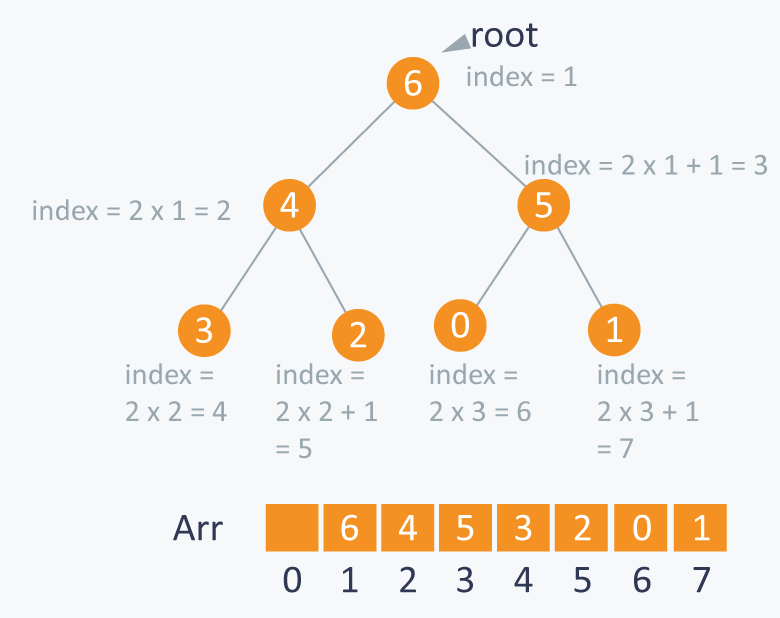
As you can see in the diagram below, we can use an array to store the nodes of the tree. Let’s say we have $$7$$ elements with values {6, 4, 5, 3, 2, 0, 1}.

Note: An array can be used to simulate a tree in the following way. If we are storing one element at index $$i$$ in array $$Arr$$, then its parent will be stored at index $$i / 2$$ (unless its a root, as root has no parent) and can be accessed by $$Arr[ i / 2 ]$$, and its left child can be accessed by $$Arr[ 2 * i ]$$ and its right child can be accessed by $$Arr[ 2 * i +1 ]$$. Index of root will be $$1$$ in an array.

There can be two types of heap:

Max Heap: In this type of heap, the value of parent node will always be greater than or equal to the value of child node across the tree and the node with highest value will be the root node of the tree.

Implementation:

Let’s assume that we have a heap having some elements which are stored in array $$Arr$$. The way to convert this array into a heap structure is the following. We pick a node in the array, check if the left sub-tree and the right sub-tree are max heaps, in themselves and the node itself is a max heap (it’s value should be greater than all the child nodes)

To do this we will implement a function that can maintain the property of max heap (i.e each element value should be greater than or equal to any of its child and smaller than or equal to its parent)

void max_heapify (int Arr[ ], int i, int N)
    {
        int left = 2*i                   //left child
        int right = 2*i +1           //right child
        if(left<= N and Arr[left] > Arr[i] )
              largest = left;
        else
             largest = i;
        if(right <= N and Arr[right] > Arr[largest] )
            largest = right;
        if(largest != i )
        {
            swap (Arr[i] , Arr[largest]);
            max_heapify (Arr, largest,N);
        } 
     }

Complexity: $$O( log N ) $$

Example:
In the diagram below,initially 1st node (root node) is violating property of max-heap as it has smaller value than its children, so we are performing max_heapify function on this node having value 4.

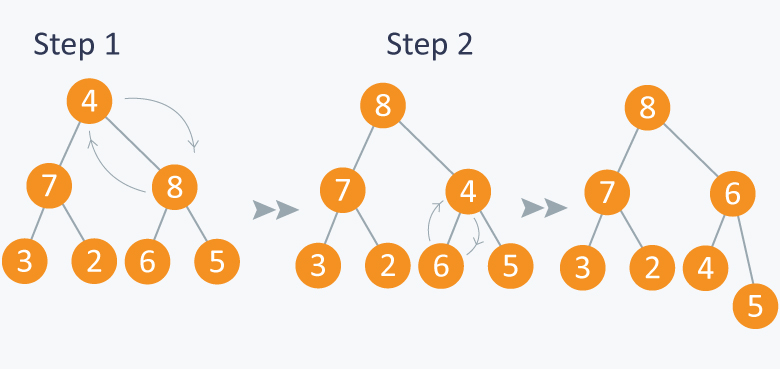
As 8 is greater than 4, so 8 is swapped with 4 and max_heapify is performed again on 4, but on different position. Now in step 2, 6 is greater than 4, so 4 is swapped with 6 and we will get a max heap, as now 4 is a leaf node, so further call to max_heapify will not create any effect on heap.

Now as we can see that we can maintain max- heap by using max_heapify function.

Before moving ahead, lets observe a property which states: A $$N$$ element heap stored in an array has leaves indexed by $$N / 2 + 1$$, $$N / 2 + 2$$ , $$N / 2 + 3$$ …. upto $$N$$.

Let’s observe this with an example:

Lets take above example of 7 elements having values {8, 7, 6, 3, 2, 4, 5}.

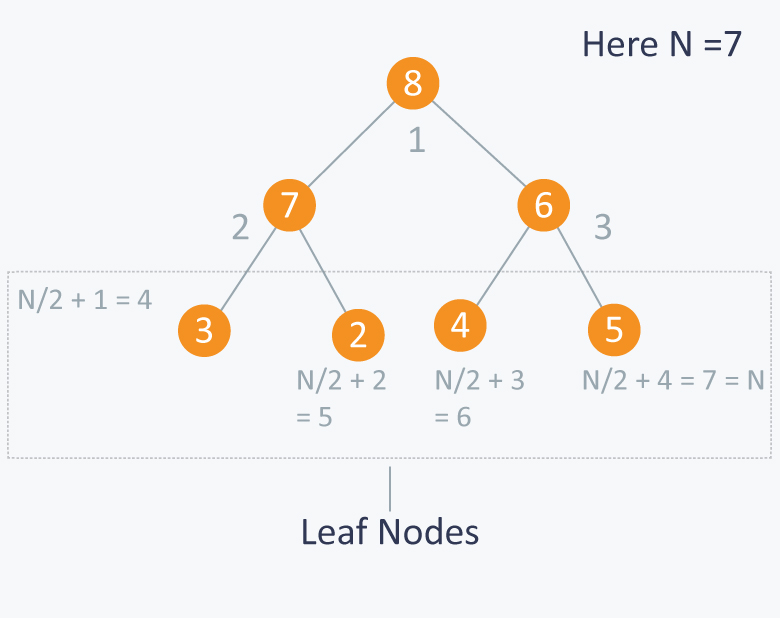
So you can see that elements 3, 2, 4, 5 are indexed by $$N / 2 + 1$$ (i.e 4), $$N / 2 + 2$$ (i.e 5 ) and $$N / 2 + 3$$ (i.e 6) and $$N / 2 + 4$$ (i.e 7) respectively.

Building MAX HEAP:

Now let’s say we have $$N$$ elements stored in the array $$Arr$$ indexed from $$1$$ to $$N$$. They are currently not following the property of max heap. So we can use max-heapify function to make a max heap out of the array.

How?

From the above property we observed that elements from $$Arr[ N/2+1 ]$$ to $$Arr[ N ]$$ are leaf nodes, and each node is a 1 element heap. We can use max_heapify function in a bottom up manner on remaining nodes, so that we can cover each node of tree.

void build_maxheap (int Arr[ ])
    {
        for(int i = N/2 ; i >= 1 ; i-- )
        {
            max_heapify (Arr, i) ;
        }
    }

Complexity: $$O(N)$$. max_heapify function has complexity $$log N$$ and the build_maxheap functions runs only $$N/2$$ times, but the amortized complexity for this function is actually linear.
For more details, you can refer this.

Example:
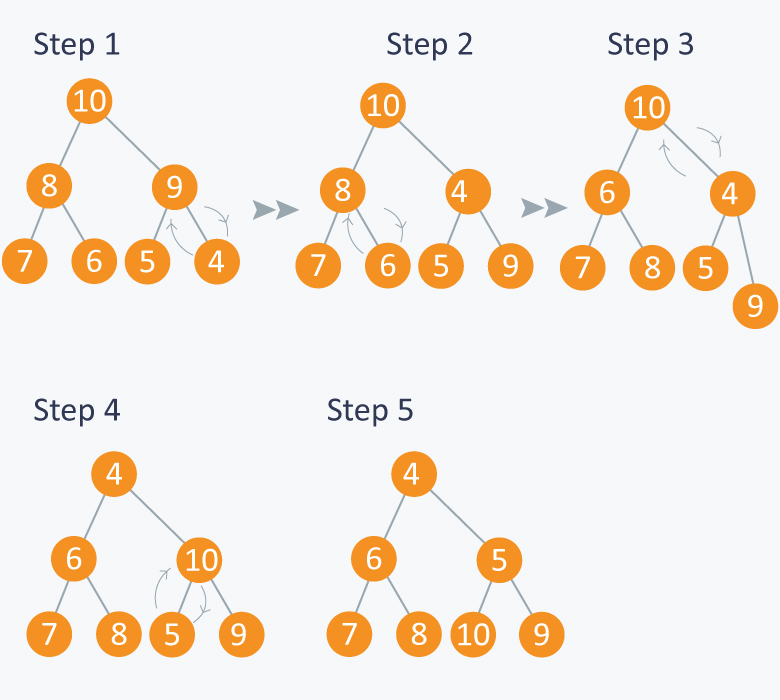
Suppose you have 7 elements stored in array $$Arr$$.

Here $$N = 7$$, so starting from node having index $$N / 2 = 3$$, (also having value 3 in the above diagram), we will call max_heapify from index $$N / 2$$ to 1.

In the diagram below:

In step 1, in max_heapify(Arr, 3), as 10 is greater than 3, 3 and 10 are swapped and further call to max_heap(Arr, 7) will have no effect as 3 is a leaf node now.

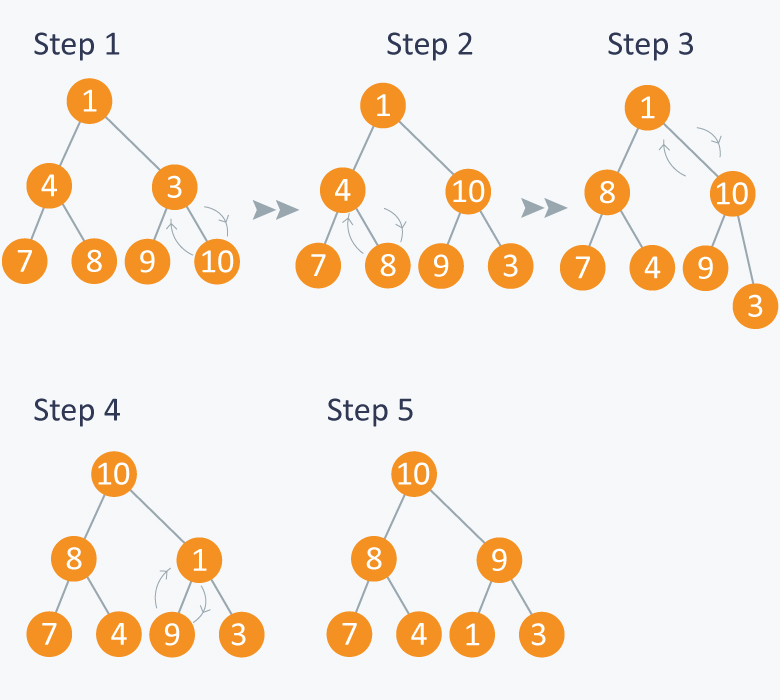
In step 2, calling max_heapify(Arr, 2) , (node indexed with 2 has value 4) , 4 is swapped with 8 and further call to max_heap(Arr, 5) will have no effect, as 4 is a leaf node now.

In step 3, calling max_heapify(Arr, 1) , (node indexed with 1 has value 1 ), 1 is swapped with 10 .

Step 4 is a subpart of step 3, as after swapping 1 with 10, again a recursive call of max_heapify(Arr, 3) will be performed , and 1 will be swapped with 9. Now further call to max_heapify(Arr, 7) will have no effect, as 1 is a leaf node now.

In step 5, we finally get a max- heap and the elements in the array Arr will be :

Min Heap: In this type of heap, the value of parent node will always be less than or equal to the value of child node across the tree and the node with lowest value will be the root node of tree.

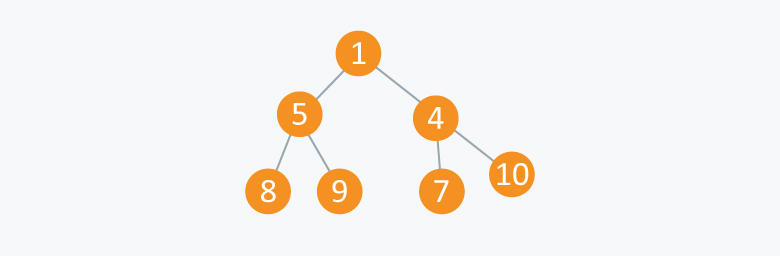
As you can see in the above diagram, each node has a value smaller than the value of their children.
We can perform same operations as performed in building max_heap.
First we will make function which can maintain the min heap property, if some element is violating it.

  void min_heapify (int Arr[ ] , int i, int N)
    {
    int left  = 2*i;
    int right = 2*i+1;
    int smallest;
    if(left <= N and Arr[left] < Arr[ i ] )
         smallest = left;
    else
        smallest = i;
    if(right <= N and Arr[right] < Arr[smallest] )
        smallest = right;
    if(smallest != i)
    {
        swap (Arr[ i ], Arr[ smallest ]);
        min_heapify (Arr, smallest,N);
    } 
    }

Complexity: $$O (log N)$$ .

Example:
Suppose you have elements stored in array $$Arr$$ {4, 5, 1, 6, 7, 3, 2}. As you can see in the diagram below, the element at index 1 is violating the property of min -heap, so performing min_heapify(Arr, 1) will maintain the min-heap.

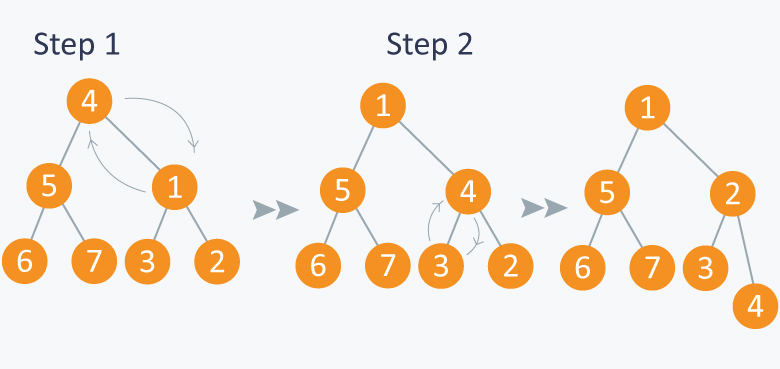
Now let’s use above function in building min-heap. We will run the above function on remaining nodes other than leaves as leaf nodes are 1 element heap.

  void build_minheap (int Arr[ ]) 
    {
        for( int i = N/2 ; i >= 1 ; i--)
        min_heapify (Arr, i);
    }

Complexity: $$O( N )$$. The complexity calculation is similar to that of building max heap.

Example:
Consider elements in array {10, 8, 9, 7, 6, 5, 4} . We will run min_heapify on nodes indexed from $$N / 2$$ to 1. Here node indexed at $$N / 2$$ has value 9. And at last, we will get a min_heap.

Heaps can be considered as partially ordered tree, as you can see in the above examples that the nodes of tree do not follow any order with their siblings(nodes on the same level). They can be mainly used when we give more priority to smallest or the largest node in the tree as we can extract these node very efficiently using heaps.

APPLICATIONS:

1) Heap Sort:

We can use heaps in sorting the elements in a specific order in efficient time.
Let’s say we want to sort elements of array $$Arr$$ in ascending order. We can use max heap to perform this operation.

Idea: We build the max heap of elements stored in $$Arr$$, and the maximum element of $$Arr$$ will always be at the root of the heap.

Leveraging this idea we can sort an array in the following manner.

Processing:

• Initially we will build a max heap of elements in $$Arr$$.

• Now the root element that is $$Arr[ 1 ]$$ contains maximum element of $$Arr$$. After that, we will exchange this element with the last element of $$Arr$$ and will again build a max heap excluding the last element which is already in its correct position and will decrease the length of heap by one.

• We will repeat the step 2, until we get all the elements in their correct position.

• We will get a sorted array.

Implementation:

Suppose there are $$N$$ elements stored in array $$Arr$$.

 void heap_sort(int Arr[ ])
    {
        int heap_size = N;
        build_maxheap(Arr);
        for(int i = N; i>=2 ; i-- )
        {
            swap(Arr[ 1 ], Arr[ i ]);
            heap_size = heap_size-1;
            max_heapify(Arr, 1, heap_size);
        }
    }

Complexity: As we know max_heapify has complexity $$O(logN)$$, build_maxheap has complexity $$O(N)$$ and we run max_heapify $$N-1$$ times in heap_sort function, therefore complexity of heap_sort function is $$O(N logN)$$.

Example:
In the diagram below,initially there is an unsorted array $$Arr$$ having 6 elements. We begin by building max-heap.

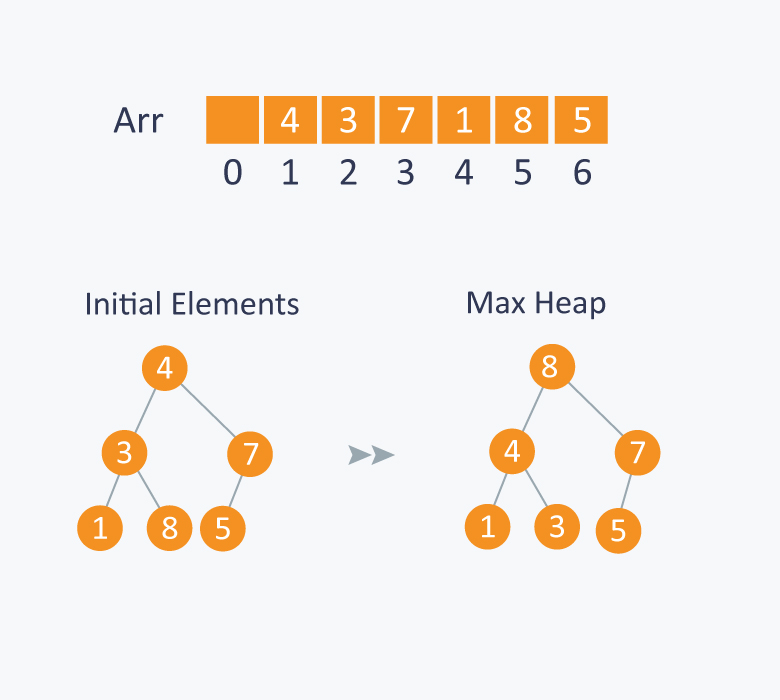
After building max-heap, the elements in the array Arr will be:

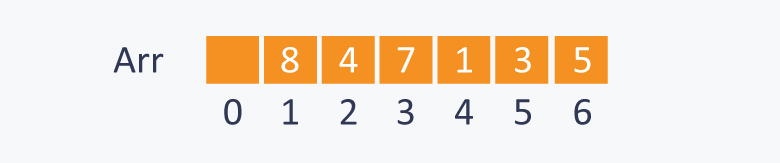
Processing:

Step 1: 8 is swapped with 5.
Step 2: 8 is disconnected from heap as 8 is in correct position now.
Step 3: Max-heap is created and 7 is swapped with 3.
Step 4: 7 is disconnected from heap.
Step 5: Max heap is created and 5 is swapped with 1.
Step 6: 5 is disconnected from heap.
Step 7: Max heap is created and 4 is swapped with 3.
Step 8: 4 is disconnected from heap.
Step 9: Max heap is created and 3 is swapped with 1.
Step 10: 3 is disconnected.

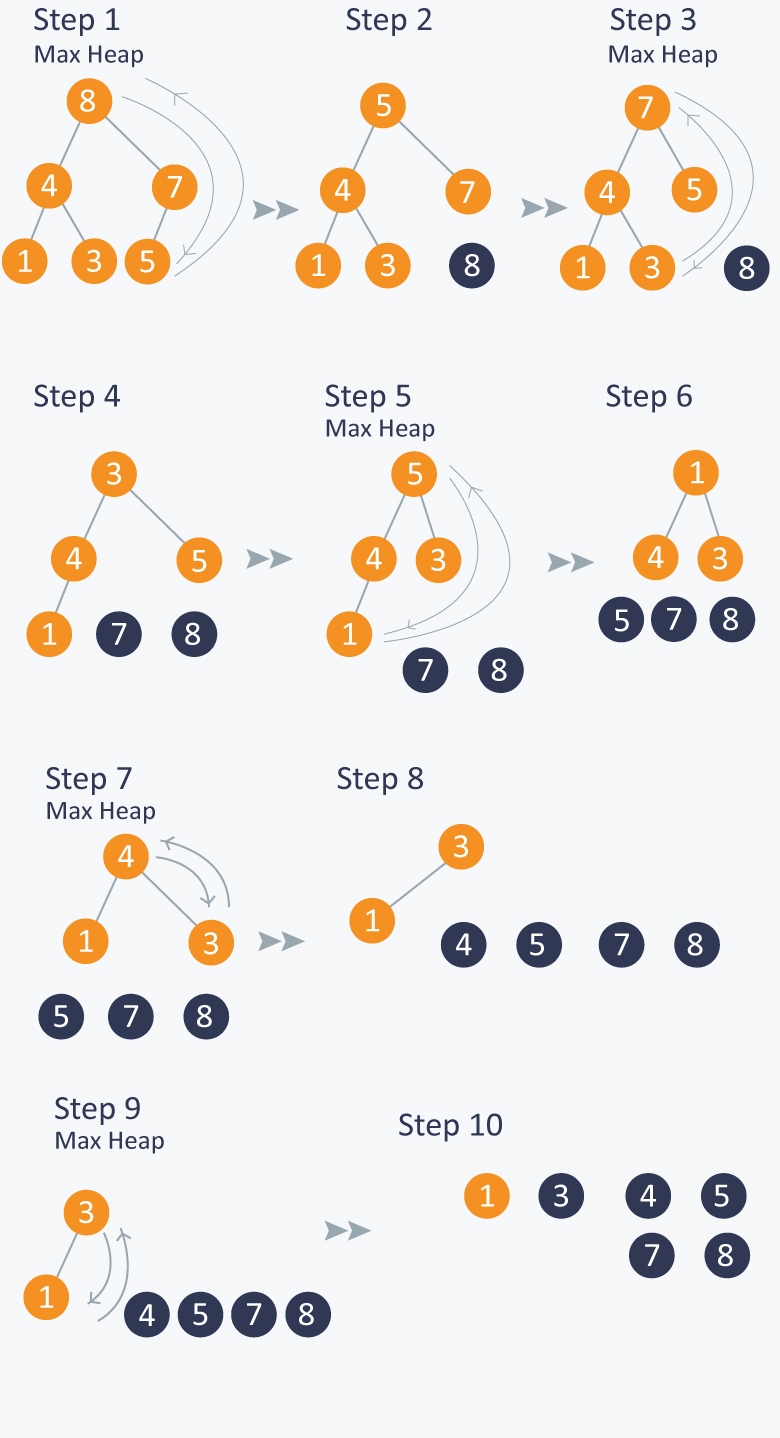
After all the steps, we will get a sorted array.

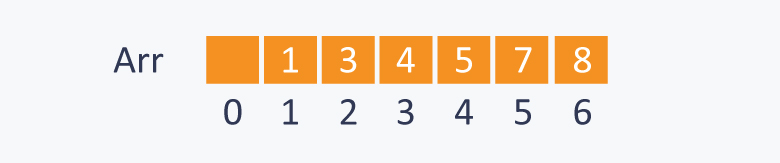
2) Priority Queue:

Priority Queue is similar to queue where we insert an element from the back and remove an element from front, but with a difference that the logical order of elements in the priority queue depends on the priority of the elements. The element with highest priority will be moved to the front of the queue and one with lowest priority will move to the back of the queue. Thus it is possible that when you enqueue an element at the back in the queue, it can move to front because of its highest priority.

Example:
Let’s say we have an array of 5 elements : {4, 8, 1, 7, 3} and we have to insert all the elements in the max-priority queue.
First as the priority queue is empty, so 4 will be inserted initially.
Now when 8 will be inserted it will moved to front as 8 is greater than 4.
While inserting 1, as it is the current minimum element in the priority queue, it will remain in the back of priority queue.
Now 7 will be inserted between 8 and 4 as 7 is smaller than 8.
Now 3 will be inserted before 1 as it is the 2^nd minimum element in the priority queue. All the steps are represented in the diagram below:

We can think of many ways to implement the priority queue.

Naive Approach:
Suppose we have $$N$$ elements and we have to insert these elements in the priority queue. We can use list and can insert elements in $$O(N)$$ time and can sort them to maintain a priority queue in $$O(N logN )$$ time.

Efficient Approach:
We can use heaps to implement the priority queue. It will take $$O(log N)$$ time to insert and delete each element in the priority queue.

Based on heap structure, priority queue also has two types max- priority queue and min - priority queue.

Let’s focus on Max Priority Queue.

Max Priority Queue is based on the structure of max heap and can perform following operations:

maximum(Arr) : It returns maximum element from the $$Arr$$.
extract_maximum (Arr) - It removes and return the maximum element from the $$Arr$$.
increase_val (Arr, i , val) - It increases the key of element stored at index $$i$$ in $$Arr$$ to new value val.
insert_val (Arr, val ) - It inserts the element with value val in Arr.

Implementation:

length = number of elements in Arr.

Maximum :

   int maximum(int Arr[ ])
        {
            return Arr[ 1 ];  //as the maximum element is the root element in the max heap.
        } 

Complexity: $$O(1)$$

Extract Maximum: In this operation, the maximum element will be returned and the last element of heap will be placed at index 1 and max_heapify will be performed on node 1 as placing last element on index 1 will violate the property of max-heap.

    int extract_maximum (int Arr[ ])
    {
        if(length == 0)
        {
    cout<< “Can’t remove element as queue is empty”;
            return -1;
        }
        int max = Arr[1];
        Arr[1] = Arr[length];
        length = length -1;
        max_heapify(Arr, 1);
        return max;
    }

Complexity: $$O(logN)$$.

Increase Value: In case increasing value of any node, it may violate the property of max-heap, so we may have to swap the parent’s value with the node’s value until we get a larger value on parent node.

   void increase_value (int Arr[ ], int i, int val)
    {
        if(val < Arr[ i ])
        {
            cout<<”New value is less than current value, can’t be inserted” <<endl;
            return;
        }
        Arr[ i ] = val;
        while( i > 1 and Arr[ i/2 ] < Arr[ i ])
        {
            swap(Arr[ i/2 ], Arr[ i ]);
            i = i/2;
        }
    }

Complexity : $$O(log N)$$.

Insert Value :

 void insert_value (int Arr[ ], int val)
    {
        length = length + 1;
        Arr[ length ] = -1;  //assuming all the numbers greater than 0 are to be inserted in queue.
        increase_val (Arr, length, val);
    }

Complexity: $$O(log N)$$.

Example:

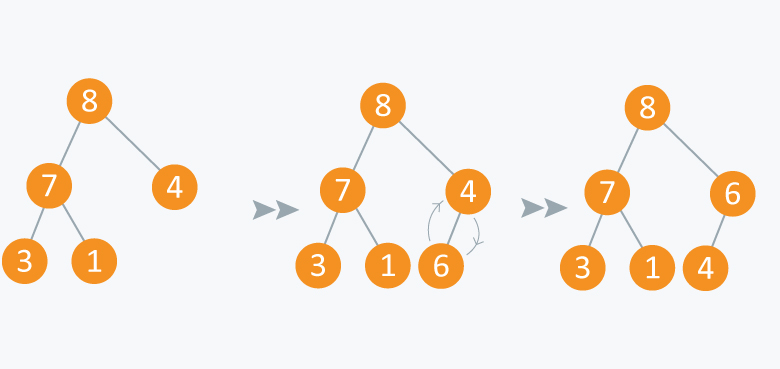
Initially there are 5 elements in priority queue.
Operation: Insert Value(Arr, 6)
In the diagram below, inserting another element having value 6 is violating the property of max-priority queue, so it is swapped with its parent having value 4, thus maintaining the max priority queue.

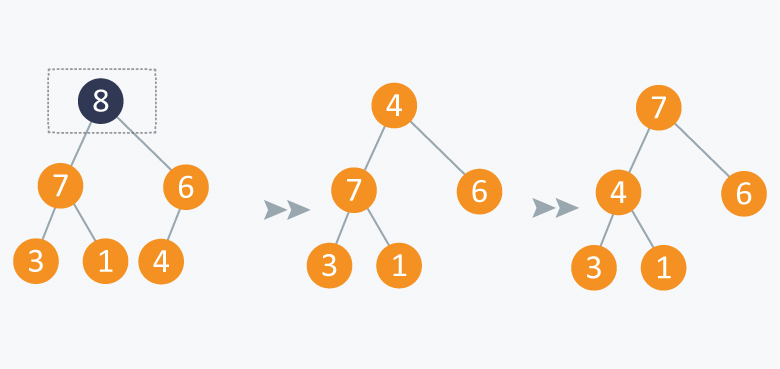
Operation: Extract Maximum:
In the diagram below, after removing 8 and placing 4 at node 1, violates the property of max-priority queue. So max_heapify(Arr, 1) will be performed which will maintain the property of max - priority queue.

As discussed above, like heaps we can use priority queues in scheduling of jobs. When there are $$N$$ jobs in queue, each having its own priority. If the job with maximum priority will be completed first and will be removed from the queue, we can use priority queue’s operation extract_maximum here. If at every instant we have to add a new job in the queue, we can use insert_value operation as it will insert the element in $$O(log N)$$ and will also maintain the property of max heap.