Binary Search Tree

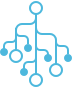
For a binary tree to be a binary search tree, the data of all the nodes in the left sub-tree of the root node should be $$\le$$ the data of the root. The data of all the nodes in the right subtree of the root node should be $$\gt$$ the data of the root.

Example

In Fig. 1, consider the root node with data = 10.

• Data in the left subtree is: $$[5, 1, 6] $$
• All data elements are $$\lt$$ $$10$$
• Data in the right subtree is: $$[19, 17]$$
• All data elements are $$\gt$$ $$10$$

Also, considering the root node with $$data = 5$$, its children also satisfy the specified ordering. Similarly, the root node with $$data = 19$$ also satisfies this ordering. When recursive, all subtrees satisfy the left and right subtree ordering.

The tree is known as a Binary Search Tree or BST.

Traversing the tree

There are mainly three types of tree traversals.

Pre-order traversal

In this traversal technique the traversal order is root-left-right i.e.

• Process data of root node
• First, traverse left subtree completely
• Then, traverse right subtree

    void perorder(struct node*root)
    {
        if(root)
        {
            printf("%d ",root->data);    //Printf root->data
            preorder(root->left);    //Go to left subtree
            preorder(root->right);     //Go to right subtree
        }
    }

Post-order traversal

In this traversal technique the traversal order is left-right-root.

• Process data of left subtree
• First, traverse right subtree
• Then, traverse root node

    void postorder(struct node*root)
    {
        if(root)
        {
            postorder(root->left);    //Go to left sub tree
            postorder(root->right);     //Go to right sub tree
            printf("%d ",root->data);    //Printf root->data
        }
    }

In-order traversal

In in-order traversal, do the following:

• First process left subtree (before processing root node)
• Then, process current root node
• Process right subtree

    void inorder(struct node*root)
    {
        if(root)
        {
            inorder(root->left);    //Go to left subtree
            printf("%d ",root->data);    //Printf root->data
            inorder(root->right);     //Go to right subtree
        }
    }

Consider the in-order traversal of a sample BST

• The 'inorder( )' procedure is called with root equal to node with $$data = 10$$
• Since the node has a left subtree, 'inorder( )' is called with root equal to node with $$data = 5$$
• Again, the node has a left subtree, so 'inorder( )' is called with $$root = 1$$

The function call stack is as follows:

• Node with $$data = 1$$ does not have a left subtree. Hence, this node is processed.
• Node with $$data = 1$$ does not have a right subtree. Hence, nothing is done.
• inorder(1) gets completed and this function call is popped from the call stack.

The stack is as follows:

• Left subtree of node with $$data = 5$$ is completely processed. Hence, this node gets processed.
• Right subtree of this node with $$data = 5$$ is non-empty. Hence, the right subtree gets processed now. 'inorder(6)' is then called.

Note

'inorder(6)' is only equivalent to saying inorder(pointer to node with $$data = 6$$). The notation has been used for brevity.

The function call stack is as follows:

Again, the node with $$data = 6$$ has no left subtree, Therefore, it can be processed and it also has no right subtree. 'inorder(6)' is then completed.

Both the left and right subtrees of node with $$data = 5$$ have been completely processed. Hence, inorder(5) is then completed.

• Now, node with $$data = 10$$ is processed
• Right subtree of this node gets processed in a similar way as described until step 10
• After right subtree of this node is completely processed, entire traversal of the BST is complete

The order in which BST in Fig. 1 is visited is: 1, 5, 6, 10, 17, 19. The in-order traversal of a BST gives a sorted ordering of the data elements that are present in the BST. This is an important property of a BST.

Insertion in BST

Consider the insertion of $$data = 20$$ in the BST.

Algorithm

Compare data of the root node and element to be inserted.

1. If the data of the root node is greater, and if a left subtree exists, then repeat step 1 with root = root of left subtree. Else, insert element as left child of current root.
2. If the data of the root node is greater, and if a right subtree exists, then repeat step 2 with root = root of right subtree. Else, insert element as right child of current root.

Implementation

    struct node* insert(struct node* root, int data)
    {
        if (root == NULL)    //If the tree is empty, return a new,single node
            return newNode(data);
        else
        {
            //Otherwise, recur down the tree 
            if (data <= root->data)
                root->left  = insert(root->left, data);
            else
                root->right = insert(root->right, data);
            //return the (unchanged) root pointer 
            return root;
        }
    }