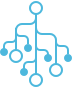
A binary tree is a structure comprising nodes, where each node has the following 3 components:
- Data element: Stores any kind of data in the node
- Left pointer: Points to the tree on the left side of node
- Right pointer: Points to the tree on the right side of the node
As the name suggests, the data element stores any kind of data in the node.
The left and right pointers point to binary trees on the left and right side of the node respectively.
If a tree is empty, it is represented by a null pointer.
The following image explains the various components of a tree.

Commonly-used terminologies
- Root: Top node in a tree
- Child: Nodes that are next to each other and connected downwards
- Parent: Converse notion of child
- Siblings: Nodes with the same parent
- Descendant: Node reachable by repeated proceeding from parent to child
- Ancestor: Node reachable by repeated proceeding from child to parent.
- Leaf: Node with no children
- Internal node: Node with at least one child
- External node: Node with no children
Structure code of a tree node
In programming, trees are declared as follows:
struct node
{
int data; //Data element
struct node * left; //Pointer to left node
struct node * right; //Pointer to right node
};
Creating nodes
Simple node
struct node root;
Pointer to a node
struct node * root;
root=(node * )malloc(sizeof(node));
In this case, you must explicitly allocate the memory of the node type to the pointer (preferred method).
Utility function returning node
struct node * newnode(int element)
{
struct node * temp=(node * )malloc(sizeof(node));
temp->data=element;
temp->left=temp->right=NULL;
return temp;
}
Maximum depth/height of a tree
The idea is to do a post-order traversal and maintain two variables to store the left depth and right depth and return max of both the depths.
int maxDepth(struct node* node)
{
if (node==NULL)
return 0;
else
{
/* compute the depth of each subtree */
int lDepth = maxDepth(node->left);
int rDepth = maxDepth(node->right);
/* use the larger one */
if (lDepth > rDepth)
return(lDepth+1);
else
return(rDepth+1);
}
}
Time complexity
$$O(n)$$
Application of trees
- a Manipulate hierarchical data
- Make information easy to search (see tree traversal)
- Manipulate sorted lists of data
- Use as a workflow for compositing digital images for visual effects
- Use in router algorithms