Binary Indexed Tree also called Fenwick Tree provides a way to represent an array of numbers in an array, allowing prefix sums to be calculated efficiently. For example, an array [2, 3, -1, 0, 6] is given, then the prefix sum of first 3 elements [2, 3, -1] is 2 + 3 + -1 = 4. Calculating prefix sum efficiently is useful in various scenarios. Let's start with a simple problem.
Given an array a[], and two types of operations are to be performed on it.
- Change the value stored at an index i. (This is called a point update operation)
- Find the sum of a prefix of length k. (This is called a range sum query)
A straightforward implementation of the above would look like this.
int a[] = {2, 1, 4, 6, -1, 5, -32, 0, 1};
void update(int i, int v) //assigns value v to a[i]
{
a[i] = v;
}
int prefixsum(int k) //calculate the sum of all a[i] such that 0 <= i < k
{
int sum = 0;
for(int i = 0; i < k; i++)
sum += a[i];
return sum;
}This is a perfect solution, but unfortunately, the time required to calculate a prefix sum is proportional to the length of the array, so this will usually time out when large numbers of such intermingled operations are performed.
One efficient solution is to use segment tree that can perform both operations in O(logN) time.
Using binary Indexed tree also, we can perform both the tasks in O(logN) time. But then why to learn another data structure when segment tree can do the work for us. It’s because binary indexed trees require less space and are very easy to implement during programming contests (the total code is not more than 8-10 lines).
Before starting with the binary indexed tree, have a look at a particular bit manipulation trick.
Isolating the last set bit

How to isolate?
x & (-x) gives the last set bit in a number x. How?
Say x=a1b(in binary) is the number whose last set bit we want to isolate.
Here a is some binary sequence of any length of 1’s and 0’s and b is some sequence of any length but of 0’s only. Remember we said we want the LAST set bit, so for that tiny intermediate 1 bit sitting between a and b to be the last set bit, b should be a sequence of 0’s only of length zero or more.
-x = 2’s complement of x = (a1b)’ + 1 = a’0b’ + 1 = a’0(0….0)’ + 1 = a’0(1...1) + 1 = a’1(0…0) = a’1b
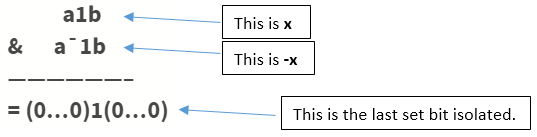
Example: x = 10(in decimal) = 1010(in binary)
The last set bit is given by x&(-x) = (10)1(0) & (01)1(0) = 0010 = 2 (in decimal)
But why do we need to isolate this weird last set bit in any number? Well, we will be seeing that as you proceed further.
Now let’s dive into Binary Indexed tree.
Basic Idea of Binary Indexed Tree:
We know the fact that each integer can be represented as the sum of powers of two. Similarly, for a given array of size N, we can maintain an array BIT[] such that, at any index we can store the sum of some numbers of the given array. This can also be called a partial sum tree.
Let’s use an example to understand how BIT[] stores partial sums.
//for ease, we make sure our given array is 1-based indexed
int a[] = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16};
The above picture shows the binary indexed tree, each enclosed box of which denotes the value BIT[index] and each BIT[index] stores partial sum of some numbers.
Notice
{ a[x], if x is odd
BIT[x] = a[1] + ... + a[x], if x is power of 2
}To generalize this every index i in the BIT[] array stores the cumulative sum from the index i to i−(1<<r)+1 (both inclusive), where r represents the last set bit in the index i.
Sum of first 12 numbers in array a[]=BIT[12]+BIT[8]=(a[12]+…+a[9])+(a[8]+…+a[1])
Similarly, sum of first 6 elements =BIT[6]+BIT[4]=(a[6]+a[5])+(a[4]+…+a[1])
Sum of first 8 elements=BIT[8]=a[8]+…+a[1]
Let’s see how to construct this tree and then we will come back to querying the tree for prefix sums.
BIT[] is an array of size = 1 + the size of the given array a[] on which we need to perform operations. Initially all values in BIT[] are equal to 0. Then we call update() operation for each element of given array to construct the Binary Indexed Tree. The update() operation is discussed below.
void update(int x, int val) //add "val" at index "x"
{
for(; x <= n; x += x&-x)
BIT[x] += val;
}It's okay if you are unable to understand how the above update() function works. Let’s take an example and try to understand it.
Suppose we call update(13, 2).
Here we see from the above figure that indices 13, 14, 16 cover index 13 and thus we need to add 2 to them also.
Initially x is 13, we update BIT[13]
BIT[13] += 2;Now isolate the last set bit of x=13(1101) and add that to x , i.e. x += x&(-x)
Last bit is of x=13(1101) is 1 which we add to x, then x=13+1=14, we update BIT[14]
BIT[14] += 2;Now 14 is 1110, isolate last bit and add to 14, x becomes 14+2=16(10000), we update BIT[16]
BIT[16] += 2;In this way, when an update() operation is performed on index x we update all the indices of BIT[] which cover index x and maintain the BIT[].
If we look at the for loop in update() operation, we can see that the loop runs at most the number of bits in index x which is restricted to be less or equal to N (the size of the given array), so we can say that the update operation takes at most O(logN) time.
How to query such structure for prefix sums? Let’s look at the query operation.
int query(int x) //returns the sum of first x elements in given array a[]
{
int sum = 0;
for(; x > 0; x -= x&-x)
sum += BIT[x];
return sum;
}The above function query() returns the sum of first x elements in given array. Let’s see how it works.
Suppose we call query(14), initially sum = 0
x is 14(1110) we add BIT[14] to our sum variable, thus sum=BIT[14]=(a[14]+a[13])
Now we isolate the last set bit from x=14(1110) and subtract it from x
Last set bit in 14(1110)is2(10), thus x=14–2=12
We add BIT[12] to our sum variable, thus sum=BIT[14]+BIT[12]=(a[14]+a[13])+(a[12]+…+a[9])
Again we isolate last set bit from x=12(1100) and subtract it from x
Last set bit in 12(1100) is 4(100), thus x=12–4=8
We add BIT[8] to our sum variable, thus
sum=BIT[14]+BIT[2]+BIT[8]=(a[14]+a[13])+(a[12]+…+a[9])+(a[8]+…+a[1])
Once again we isolate last set bit from x=8(1000) and subtract it from x
Last set bit in 8(1000) is 8(1000), thus x=8–8=0
Since x=0, the for loop breaks and we return the prefix sum.
Talking about time complexity, again we can see that the loop iterates at most the number of bits in x which will be at most N (the size of the given array). Thus, the *query operation takes O(logN) time *.
Here’s the full program to solve efficiently, the problem that we discussed at the start of this article.
int BIT[1000], a[1000], n;
void update(int x, int val)
{
for(; x <= n; x += x&-x)
BIT[x] += val;
}
int query(int x)
{
int sum = 0;
for(; x > 0; x -= x&-x)
sum += BIT[x];
return sum;
}
int main()
{
scanf(“%d”, &n);
int i;
for(i = 1; i <= n; i++)
{
scanf(“%d”, &a[i]);
update(i, a[i]);
}
printf(“sum of first 10 elements is %d\n”, query(10));
printf(“sum of all elements in range [2, 7] is %d\n”, query(7) – query(2-1));
return 0;
}When to use Binary Indexed Tree?
Before going for Binary Indexed tree to perform operations over range, one must confirm that the operation or the function is:
Associative. i.e f(f(a,b),c)=f(a,f(b,c)) this is true even for seg-tree
Has an inverse. eg:
- Addition has inverse subtraction (this example we have discussed)
- Multiplication has inverse division
- gcd() has no inverse, so we can’t use BIT to calculate range gcd’s
- Sum of matrices has inverse
- Product of matrices would have inverse if it is given that matrices are degenerate i.e. determinant of any matrix is not equal to 0
Space Complexity: O(N) for declaring another array of size N
Time Complexity: O(logN) for each operation(update and query as well)
Applications:
- Binary Indexed trees are used to implement the arithmetic coding algorithm. Development of operations it supports were primarily motivated by use in that case.
- Binary Indexed Tree can be used to count inversions in an array in O(NlogN) time.