Merge Sort

Merge sort is a divide-and-conquer algorithm based on the idea of breaking down a list into several sub-lists until each sublist consists of a single element and merging those sublists in a manner that results into a sorted list.

Idea:

• Divide the unsorted list into $$N$$ sublists, each containing $$1$$ element.
• Take adjacent pairs of two singleton lists and merge them to form a list of 2 elements. $$N$$ will now convert into $$N/2$$ lists of size 2.
• Repeat the process till a single sorted list of obtained.

While comparing two sublists for merging, the first element of both lists is taken into consideration. While sorting in ascending order, the element that is of a lesser value becomes a new element of the sorted list. This procedure is repeated until both the smaller sublists are empty and the new combined sublist comprises all the elements of both the sublists.

Let’s consider the following image

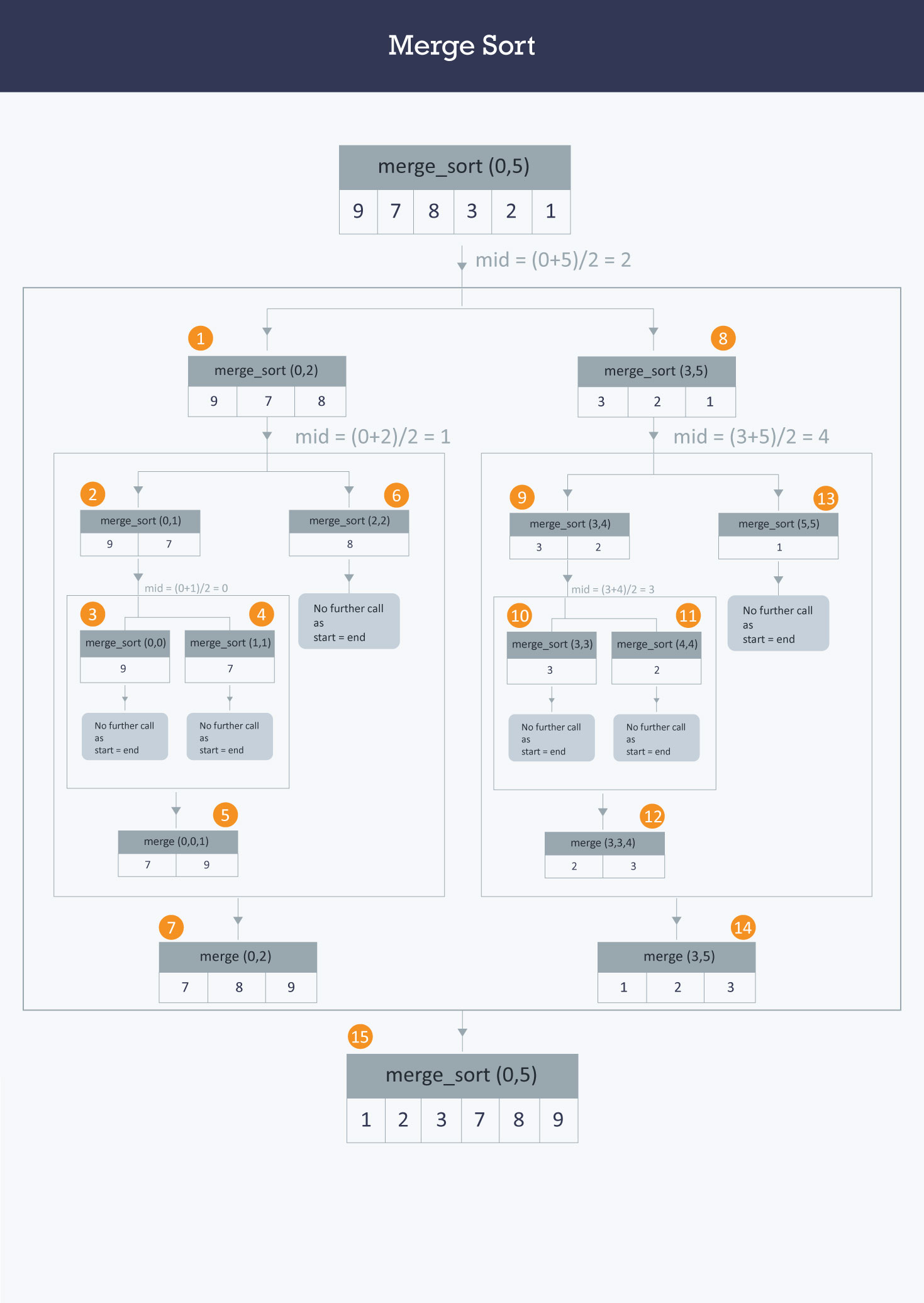
As one may understand from the image above, at each step a list of size $$M$$ is being divided into $$2$$ sublists of size $$M / 2$$, until no further division can be done. To understand better, consider a smaller array $$A$$ containing the elements $$(9,7,8)$$.

At the first step this list of size $$3$$ is divided into $$2$$ sublists the first consisting of elements $$(9,7)$$ and the second one being $$(8)$$. Now, the first list consisting of elements $$(9,7)$$ is further divided into $$2$$ sublists consisting of elements $$(9)$$ and $$(7)$$ respectively.

As no further breakdown of this list can be done, as each sublist consists of a maximum of $$1$$ element, we now start to merge these lists. The $$2$$ sub-lists formed in the last step are then merged together in sorted order using the procedure mentioned above leading to a new list $$(7,9)$$. Backtracking further, we then need to merge the list consisting of element $$(8)$$ too with this list, leading to the new sorted list $$(7,8,9)$$.

An implementation has been provided below :

 void merge(int A[ ] , int start, int mid, int end) {
 //stores the starting position of both parts in temporary variables.
int p = start ,q = mid+1;

int Arr[end-start+1] , k=0;

for(int i = start ;i <= end ;i++) {
    if(p > mid)      //checks if first part comes to an end or not .
       Arr[ k++ ] = A[ q++] ;

   else if ( q > end)   //checks if second part comes to an end or not
       Arr[ k++ ] = A[ p++ ];

   else if( A[ p ] < A[ q ])     //checks which part has smaller element.
      Arr[ k++ ] = A[ p++ ];

   else
      Arr[ k++ ] = A[ q++];
 }
  for (int p=0 ; p< k ;p ++) {
   /* Now the real array has elements in sorted manner including both 
        parts.*/
     A[ start++ ] = Arr[ p ] ;                          
  }
}

Here, in merge function, we will merge two parts of the arrays where one part has starting and ending positions from start to mid respectively and another part has positions from mid+1 to the end.

A beginning is made from the starting parts of both arrays. i.e. p and q. Then the respective elements of both the parts are compared and the one with the smaller value will be stored in the auxiliary array (Arr[ ]). If at some condition ,one part comes to end ,then all the elements of another part of array are added in the auxiliary array in the same order they exist.

Now consider the following 2 branched recursive function :

   void merge_sort (int A[ ] , int start , int end )
   {
           if( start < end ) {
           int mid = (start + end ) / 2 ;           // defines the current array in 2 parts .
           merge_sort (A, start , mid ) ;                 // sort the 1st part of array .
           merge_sort (A,mid+1 , end ) ;              // sort the 2nd part of array.

         // merge the both parts by comparing elements of both the parts.
          merge(A,start , mid , end );   
   }                    
}

Time Complexity:
The list of size $$N$$ is divided into a max of $$log N$$ parts, and the merging of all sublists into a single list takes $$O(N)$$ time, the worst case run time of this algorithm is $$O(N Log N)$$