Heap Sort
Heaps can be used in sorting an array. In max-heaps, maximum element will always be at the root. Heap Sort uses this property of heap to sort the array.
Consider an array $$ Arr $$ which is to be sorted using Heap Sort.
- Initially build a max heap of elements in $$ Arr $$.
- The root element, that is $$Arr[1]$$, will contain maximum element of $$ Arr $$. After that, swap this element with the last element of $$ Arr $$ and heapify the max heap excluding the last element which is already in its correct position and then decrease the length of heap by one.
- Repeat the step 2, until all the elements are in their correct position.
Implementation:
void heap_sort(int Arr[ ])
{
int heap_size = N;
build_maxheap(Arr);
for(int i = N; i >= 2 ; i-- )
{
swap|(Arr[ 1 ], Arr[ i ]);
heap_size = heap_size - 1;
max_heapify(Arr, 1, heap_size);
}
}
Complexity:
max_heapify has complexity $$ O(logN) $$, build_maxheap has complexity $$O(N)$$ and we run max_heapify $$N-1$$ times in heap_sort function, therefore complexity of heap_sort function is $$O(NlogN)$$.
Example:
In the diagram below,initially there is an unsorted array Arr having 6 elements and then max-heap will be built.

After building max-heap, the elements in the array $$Arr$$ will be:

Step 1: 8 is swapped with 5.
Step 2: 8 is disconnected from heap as 8 is in correct position now and.
Step 3: Max-heap is created and 7 is swapped with 3.
Step 4: 7 is disconnected from heap.
Step 5: Max heap is created and 5 is swapped with 1.
Step 6: 5 is disconnected from heap.
Step 7: Max heap is created and 4 is swapped with 3.
Step 8: 4 is disconnected from heap.
Step 9: Max heap is created and 3 is swapped with 1.
Step 10: 3 is disconnected.
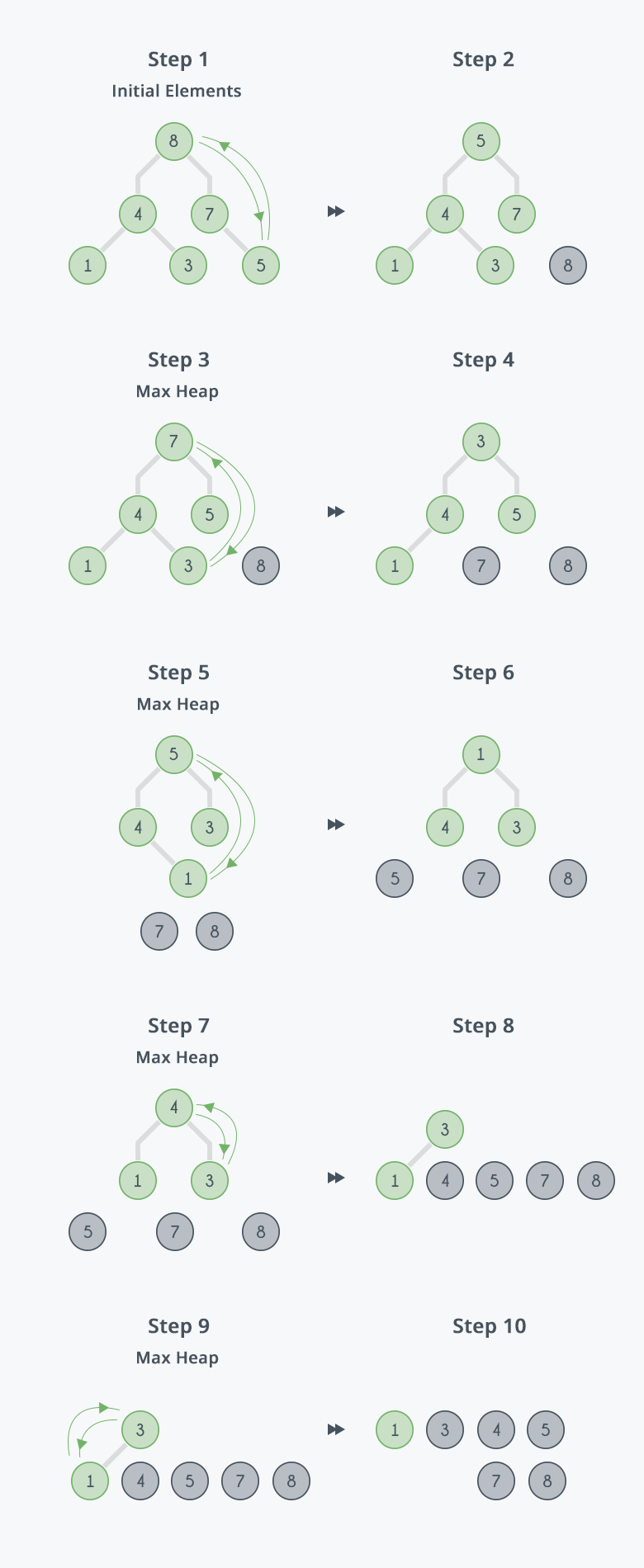
After all the steps, we will get a sorted array.


