Topological sorting of vertices of a Directed Acyclic Graph is an ordering of the vertices $$v_1, v_2, ... v_n$$ in such a way, that if there is an edge directed towards vertex $$v_j$$ from vertex $$v_i$$, then $$v_i$$ comes before $$v_j$$. For example consider the graph given below:
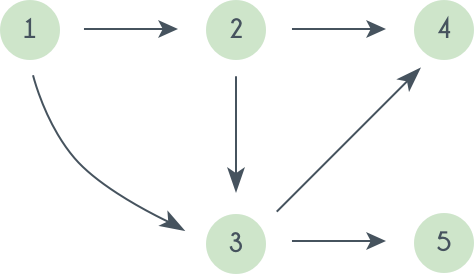
A topological sorting of this graph is: $$1$$ $$2$$ $$3$$ $$4$$ $$5$$
There are multiple topological sorting possible for a graph. For the graph given above one another topological sorting is: $$1$$ $$2$$ $$3$$ $$5$$ $$4$$
In order to have a topological sorting the graph must not contain any cycles. In order to prove it, let's assume there is a cycle made of the vertices $$v_1, v_2, v_3 ... v_n$$. That means there is a directed edge between $$v_i$$ and $$v_{i+1}$$ $$(1 \le i \lt n)$$ and between $$v_n$$ and $$v_1$$. So now, if we do topological sorting then $$v_n$$ must come before $$v_1$$ because of the directed edge from $$v_n$$ to $$v_1$$. Clearly, $$v_{i+1}$$ will come after $$v_i$$, because of the directed from $$v_i$$ to $$v_{i+1}$$, that means $$v_1$$ must come before $$v_n$$. Well, clearly we've reached a contradiction, here. So topological sorting can be achieved for only directed and acyclic graphs.
Le'ts see how we can find a topological sorting in a graph. So basically we want to find a permutation of the vertices in which for every vertex $$v_i$$, all the vertices $$v_j$$ having edges coming out and directed towards $$v_i$$ comes before $$v_i$$. We'll maintain an array $$T$$ that will denote our topological sorting. So, let's say for a graph having $$N$$ vertices, we have an array $$in\_degree[]$$ of size $$N$$ whose $$i^{th}$$ element tells the number of vertices which are not already inserted in $$T$$ and there is an edge from them incident on vertex numbered $$i$$. We'll append vertices $$v_i$$ to the array $$T$$, and when we do that we'll decrease the value of $$in\_degree[v_j]$$ by $$1$$ for every edge from $$v_i$$ to $$v_j$$. Doing this will mean that we have inserted one vertex having edge directed towards $$v_j$$. So at any point we can insert only those vertices for which the value of $$in\_degree[]$$ is $$0$$.
The algorithm using a BFS traversal is given below:
topological_sort(N, adj[N][N])
T = []
visited = []
in_degree = []
for i = 0 to N
in_degree[i] = visited[i] = 0
for i = 0 to N
for j = 0 to N
if adj[i][j] is TRUE
in_degree[j] = in_degree[j] + 1
for i = 0 to N
if in_degree[i] is 0
enqueue(Queue, i)
visited[i] = TRUE
while Queue is not Empty
vertex = get_front(Queue)
dequeue(Queue)
T.append(vertex)
for j = 0 to N
if adj[vertex][j] is TRUE and visited[j] is FALSE
in_degree[j] = in_degree[j] - 1
if in_degree[j] is 0
enqueue(Queue, j)
visited[j] = TRUE
return T
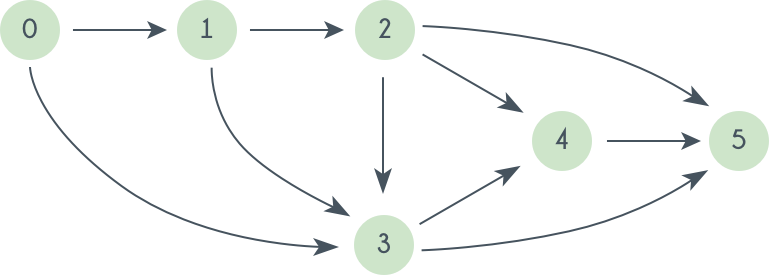
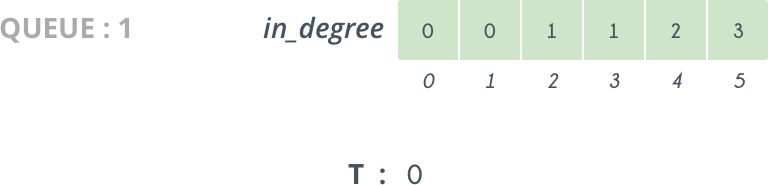
Initially $$in\_degree[0] = 0$$ and $$T$$ is empty

So, we delete $$0$$ from $$Queue$$ and append it to $$T$$. The vertices directly connected to $$0$$ are $$1$$ and $$2$$ so we decrease their $$in\_degree[]$$ by $$1$$. So, now $$in\_degree[ 1 ] = 0$$ and so $$1$$ is pushed in $$Queue$$.
Next we delete $$1$$ from $$Queue$$ and append it to $$T$$. Doing this we decrease $$in\_degree[ 2 ]$$ by $$1$$, and now it becomes $$0$$ and $$2$$ is pushed into $$Queue$$.

So, we continue doing like this, and further iterations looks like as follows:
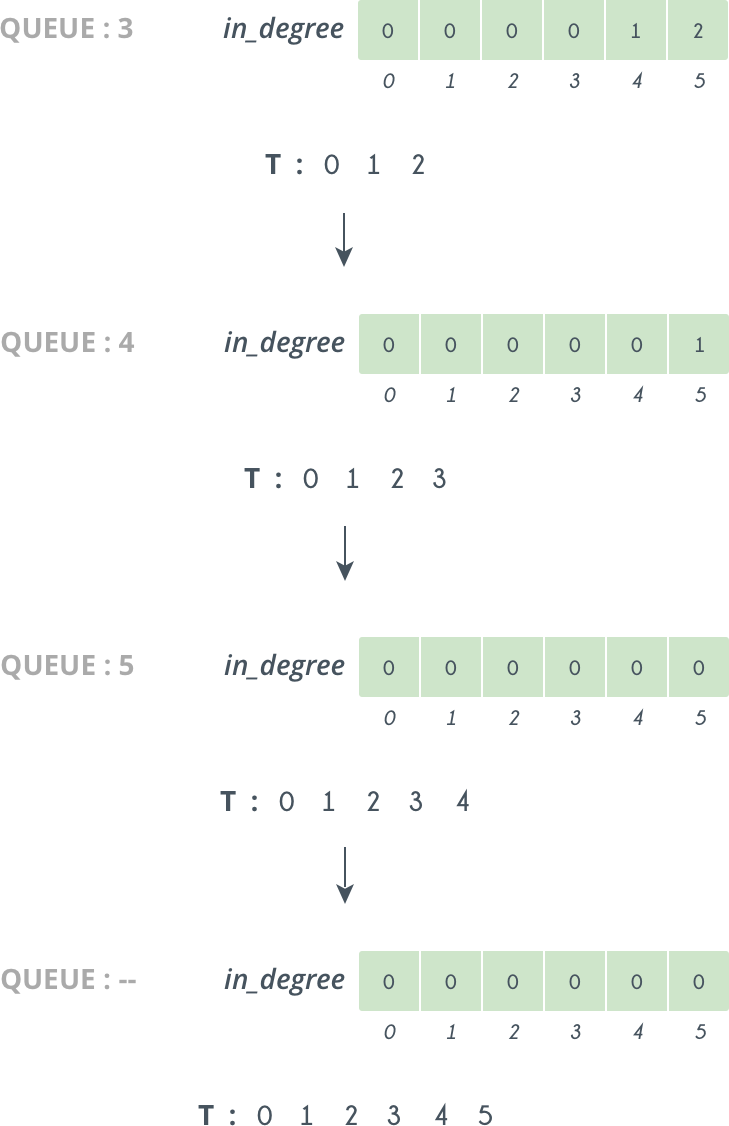
So at last we get our Topological sorting in $$T$$ i.e. : $$0$$, $$1$$, $$2$$, $$3$$, $$4$$, $$5$$
Solution using a DFS traversal, unlike the one using BFS, does not need any special $$in\_degree[]$$ array. Following is the pseudo code of the DFS solution:
T = []
visited = []
topological_sort( cur_vert, N, adj[][] ){
visited[cur_vert] = true
for i = 0 to N
if adj[cur_vert][i] is true and visited[i] is false
topological_sort(i)
T.insert_in_beginning(cur_vert)
}


