Strings can essentially be viewed as the most important and common topics for a variety of programming problems. String processing has a variety of real world applications too, such as:
- Search Engines
- Genome Analysis
- Data Analytics
All the content presented to us in textual form can be visualized as nothing but just strings.
Tries:
Tries are an extremely special and useful data-structure that are based on the prefix of a string. They are used to represent the “Retrieval” of data and thus the name Trie.
Prefix : What is prefix:
The prefix of a string is nothing but any $$n$$ letters $$n \le |S|$$ that can be considered beginning strictly from the starting of a string. For example , the word “abacaba” has the following prefixes:
a
ab
aba
abac
abaca
abacab
A Trie is a special data structure used to store strings that can be visualized like a graph. It consists of nodes and edges. Each node consists of at max 26 children and edges connect each parent node to its children. These 26 pointers are nothing but pointers for each of the 26 letters of the English alphabet A separate edge is maintained for every edge.
Strings are stored in a top to bottom manner on the basis of their prefix in a trie. All prefixes of length 1 are stored at until level 1, all prefixes of length 2 are sorted at until level 2 and so on.
For example , consider the following diagram :
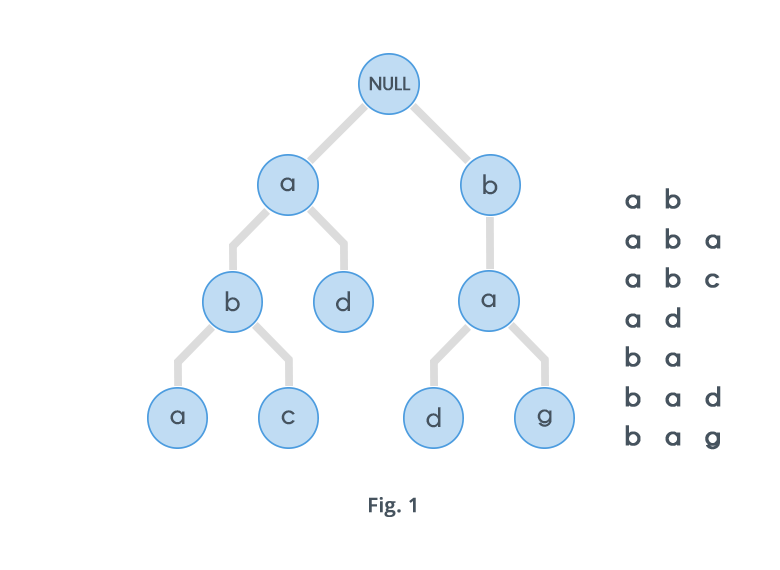
Now, one would be wondering why to use a data structure such as a trie for processing a single string? Actually, Tries are generally used on groups of strings, rather than a single string. When given multiple strings , we can solve a variety of problems based on them. For example, consider an English dictionary and a single string $$s$$, find the prefix of maximum length from the dictionary strings matching the string $$s$$. Solving this problem using a naive approach would require us to match the prefix of the given string with the prefix of every other word in the dictionary and note the maximum. The is an expensive process considering the amount of time it would take. Tries can solve this problem in much more efficient way.
Before processing each Query of the type where we need to search the length of the longest prefix, we first need to add all the existing words into the dictionary. A Trie consists of a special node called the root node. This node doesn't have any incoming edges. It only contains 26 outgoing edfes for each letter in the alphabet and is the root of the Trie.
So, the insertion of any string into a Trie starts from the root node. All prefixes of length one are direct children of the root node. In addition, all prefixes of length 2 become children of the nodes existing at level one.
The pseudo code for insertion of a string into a tire would look as follows:
void insert(String s)
{
for(every char in string s)
{
if(child node belonging to current char is null)
{
child node=new Node();
}
current_node=child_node;
}
}
The pseudo code to check wether a single word exists in a dictionary of words or not is as follows:
boolean check(String s)
{
for(every char in String s)
{
if(child node is null)
{
return false;
}
}
return true;
}